题目内容
15.用适当的方法证明下列命题:(1)$\sqrt{b+1}-\sqrt{b}<\sqrt{b-1}-\sqrt{b-2}(b≥2)$
(2)设a,b,c∈(0,+∞),求证:三个数中$a+\frac{1}{b},c+\frac{1}{a},b+\frac{1}{c}$至少有一个不小于2.
分析 (1)用分析法即可证明.
(2)假设$a+\frac{1}{b},c+\frac{1}{a},b+\frac{1}{c}$都小于2,则a+$\frac{1}{b}$+c+$\frac{1}{a}$+b+$\frac{1}{c}$<6,再结合基本不等式,引出矛盾,即可得出结论
解答 解:(1)要证:$\sqrt{b+1}$-$\sqrt{b}$<$\sqrt{b-1}$-$\sqrt{b-2}$(b≥2),
只要证$\sqrt{b+1}$+$\sqrt{b-2}$<$\sqrt{b}$+$\sqrt{b-1}$,
只要证($\sqrt{b+1}$+$\sqrt{b-2}$)2<($\sqrt{b}$+$\sqrt{b-1}$)2,
即2b-1+2$\sqrt{{b}^{2}-b-2}$<2b-1+2$\sqrt{{b}^{2}-b}$
只要证$\sqrt{{b}^{2}-b-2}$<$\sqrt{{b}^{2}-b}$
只要证b2-b-2<b2-b,
只要证-2<0,
显然-2<0成立,
故原不等式成立;
(2)证明:假设$a+\frac{1}{b},c+\frac{1}{a},b+\frac{1}{c}$都小于2,则a+$\frac{1}{b}$+c+$\frac{1}{a}$+b+$\frac{1}{c}$<6.
∵a,b,c均大于0,
∴a+$\frac{1}{b}$+c+$\frac{1}{a}$+b+$\frac{1}{c}$≥2+2+2+2=6,矛盾.
∴a+$\frac{1}{b}$+c+$\frac{1}{a}$+b+$\frac{1}{c}$中至少有一个不小于2.
点评 本题考查了利用分析法证明不等式成立,反证法证明数学命题的方法和步骤,把要证的结论进行否定,得到要证的结论的反面,是解题的突破口关键是转化,属于中档题.

| A. | $\frac{3}{2}$ | B. | $-\frac{11}{3}$ | C. | 3 | D. | -3 |
| A. | 2 | B. | 3 | C. | -1 | D. | 1 |
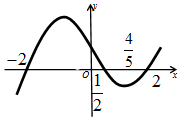
| A. | $\frac{1}{2}$为f(x)的极大值点 | B. | -2为f(x)的极大值点 | ||
| C. | 2为f(x)的极大值 | D. | $\frac{4}{5}$为f(x)的极小值点 |
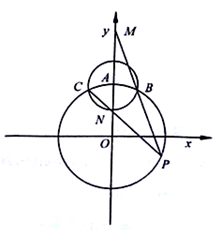 如图,在平面直角坐标系xOy中,圆O:x2+y2=4与y轴的正半轴交于点A,以A为圆心的圆x2+(y-2)2=r2(r>0)与圆O交于B、C两点.
如图,在平面直角坐标系xOy中,圆O:x2+y2=4与y轴的正半轴交于点A,以A为圆心的圆x2+(y-2)2=r2(r>0)与圆O交于B、C两点.