题目内容
3．已知函数f（x）=2ln（3x）+8x，则$\underset{lim}{△x→0}$$\frac{f（1-2△x）-f（1）}{△x}$的值为（ ）| A． | 10 | B． | -10 | C． | -20 | D． | 20 |
分析 利用导数的定义与运算法则即可得出．
解答 解：函数f（x）=2ln（3x）+8x，
∴f′（x）=$\frac{2}{x}$+8，
∴f′（1）=10，
∴$\underset{lim}{△x→0}$$\frac{f（1-2△x）-f（1）}{△x}$=-2$\underset{lim}{△x→0}$$\frac{f（1-2△x）-f（1）}{-2△x}$=-2f′（1）=-20，
故选：C
点评 本题考查了导数的定义与运算法则，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
11．若复数2-bi（b∈R）的实部与虚部之和为零，则b的值为（ ）
| A． | 2 | B． | $\frac{2}{3}$ | C． | -$\frac{2}{3}$ | D． | -2 |
18．要得到$y=cos（4x-\frac{π}{3}）$的图象，只需将函数y=cos4x图象（ ）
| A． | 向左平移$\frac{π}{12}$个单位 | B． | 向右平移$\frac{π}{12}$个单位 | ||
| C． | 向左平移$\frac{π}{3}$个单位 | D． | 向右平移$\frac{π}{3}$个单位 |
8．已知椭圆$\frac{x^2}{m+1}+{y^2}=1（m＞0）$的两个焦点是F1，F2，E是直线y=x+2与椭圆的一个公共点，当|EF1|+|EF2|取得最小值时椭圆的离心率为（ ）
| A． | $\frac{2}{3}$ | B． | $\frac{{\sqrt{3}}}{3}$ | C． | $\frac{{\sqrt{2}}}{3}$ | D． | $\frac{{\sqrt{6}}}{3}$ |
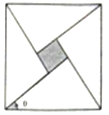我国古代数学家赵爽利用“勾股圈方图”巧妙的证明了勾股定理，成就了我国古代数学的骄傲，后人称之为“赵爽弦图”．他是由四个全等的直角三角形和中间的一个小正方形拼成的一个大正方形，若直角三角形中较小的锐角记为θ，大正方形的面积为25，小正方形的面积为1，则$sin\frac{θ}{2}+cos\frac{θ}{2}$=$\frac{{2\sqrt{10}}}{5}$．