题目内容
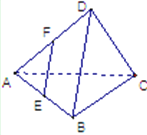已知空间四面体D-ABC的每条边都等于1，点E，F分别是AB，AD的中点，则| FE |
| DC |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
考点：平面向量数量积的运算
专题：平面向量及应用
分析：根据题意知EF∥BD，且EF=
BD，所以根据共线向量基本定理可得：
=
，因为|
|=|
|=1，∠BDC=60°，所以这就可以求出
•
了．
| 1 |
| 2 |
| FE |
| 1 |
| 2 |
| DB |
| DB |
| DC |
| FE |
| DC |
解答：
解：由已知条件得：EF∥BD，且EF=
BD，∴
=
；
∴
•
=
•
=
．
故选：A．
解：由已知条件得：EF∥BD，且EF=| 1 |
| 2 |
| FE |
| 1 |
| 2 |
| DB |
∴
| FE |
| DC |
| 1 |
| 2 |
| DB |
| DC |
| 1 |
| 4 |
故选：A．
点评：本题考查共线向量基本定理，向量数量积的计算公式．
练习册系列答案
相关题目
已知函数f（x）=
，若不等式f（m2+1）≥f（tm-1）对任意实数m恒成立，则实数t的取值范围（ ）
|
A、(-2
| ||||
B、[-2
| ||||
C、(-∞， -2
| ||||
D、(-∞， -2
|
如图，
+
-
等于（ ）
| AB |
| BC |
| AD |
A、
| ||
B、
| ||
C、
| ||
D、
|
下面几何体是由（ ）旋转得到的．
A、 |
B、 |
C、 |
D、 |
已知f′（x）是函数f（x）=cosx的导函数，若g（x）=f（x）+
f′（x），则使函数y=g（x+a）是偶函数的一个a值是（ ）
| 3 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
等比数列前三项分别为x，2x+2，3x+3，则第四项为（ ）
A、-
| ||
B、
| ||
| C、4x+4 | ||
| D、（2x+2）÷[（3x+3）x] |
在四棱锥P-ABCD中，四边形ABCD正方形，PA⊥平面ABCD，且PA=AB=2，E为PD的中点．