题目内容
已知f′(x)是函数f(x)=cosx的导函数,若g(x)=f(x)+
f′(x),则使函数y=g(x+a)是偶函数的一个a值是( )
| 3 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
考点:导数的运算
专题:导数的概念及应用
分析:先求导,得到f′(x),再求出g(x)=2cos(x+
),再得到y=2cos(x+a+
),根据偶函数的性质得到结论.
| π |
| 3 |
| π |
| 3 |
解答:
解:∵f′(x)是函数f(x)=cosx的导函数,
∴f′(x)=-sinx,
∴g(x)=f(x)+
f′(x)=cosx-
sinx=2cos(x+
),
∴y=g(x+a)=2cos(x+a+
),
∵y=g(x+a)是偶函数,
∴a+
=kπ,(k∈z)
∴a=-
+kπ,(k∈z)
当k=0时,a=-
.
故选:D
∴f′(x)=-sinx,
∴g(x)=f(x)+
| 3 |
| 3 |
| π |
| 3 |
∴y=g(x+a)=2cos(x+a+
| π |
| 3 |
∵y=g(x+a)是偶函数,
∴a+
| π |
| 3 |
∴a=-
| π |
| 3 |
当k=0时,a=-
| π |
| 3 |
故选:D
点评:本题主要考查了求导的公式,以及三角函数的和差转化,以及偶函数的性质,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
P是双曲线C:
-
=1上的一个点,F1,F2是C的两个焦点,若|PF1|=5,则|PF2|=( )
| x2 |
| 4 |
| y2 |
| 12 |
| A、9或1 | B、7或3 | C、9 | D、7 |
集合M由正整数的平方组成,即M={1,4,9,16,25,…},若对某集合中的任意两个元素进行某种运算,运算结果仍在此集合中,则称此集合对该运算是封闭的,M对下列运算是封闭的是( )
| A、加法 | B、减法 | C、乘法 | D、除法 |
对任意实数a,b定义运算“⊙“:a⊙b=
,设f(x)=(x2-1)⊙(4+x)+k,若函数f(x)的图象与x轴恰有三个交点,则k的取值范围是( )
|
| A、[-2,1) |
| B、[0,1] |
| C、(0,1] |
| D、(-2,1) |
某几何体的三视图如图所示,则其体积为( )


A、
| ||
B、
| ||
C、
| ||
| D、π |
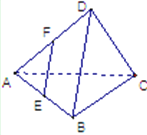 已知空间四面体D-ABC的每条边都等于1,点E,F分别是AB,AD的中点,则
已知空间四面体D-ABC的每条边都等于1,点E,F分别是AB,AD的中点,则| FE |
| DC |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
 已知函数y=
已知函数y=