题目内容
已知函数f(x)=
,若不等式f(m2+1)≥f(tm-1)对任意实数m恒成立,则实数t的取值范围( )
|
A、(-2
| ||||
B、[-2
| ||||
C、(-∞, -2
| ||||
D、(-∞, -2
|
考点:分段函数的应用
专题:计算题,函数的性质及应用
分析:函数f(x)=
在R上单调递增,不等式f(m2+1)≥f(tm-1)对任意实数m恒成立,可得不等式m2-tm+2≥0对任意实数m恒成立,即可求得结论.
|
解答:
解:函数f(x)=
在R上单调递增,
∵不等式f(m2+1)≥f(tm-1)对任意实数m恒成立,
∴不等式m2-tm+2≥0对任意实数m恒成立,
∴△=t2-8≤0,
∴-2
≤t≤2
,
故选:B.
|
∵不等式f(m2+1)≥f(tm-1)对任意实数m恒成立,
∴不等式m2-tm+2≥0对任意实数m恒成立,
∴△=t2-8≤0,
∴-2
| 2 |
| 2 |
故选:B.
点评:本题考查分段函数的应用,考查函数的单调性,考查恒成立问题,属于中档题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
已知函数f(x)=
,对一切实数R都有
>0,则a的取值范围是( )
|
| f(x1)-f(x2) |
| x1-x2 |
| A、(0,1) |
| B、(0,1] |
| C、[-1,0) |
| D、(-1,0) |
已知x∈[-2,2]、f(x)=2x分别是双曲线f(x)的左、右焦点,f(x)=2为双曲线上的一点,若∠F1PF2=90°,且△F1PF2的三边长成等差数列,则双曲线的离心率是( )
| A、2 | B、3 | C、4 | D、5 |
P是双曲线C:
-
=1上的一个点,F1,F2是C的两个焦点,若|PF1|=5,则|PF2|=( )
| x2 |
| 4 |
| y2 |
| 12 |
| A、9或1 | B、7或3 | C、9 | D、7 |
若函数f(x)=x2-2x-4lnx的导函数为f′(x),则f′(x)>0的解集为( )
| A、(0,+∞) |
| B、(-1,0)∪(2,+∞) |
| C、(-1,0) |
| D、(2,+∞) |
已知命题p:?x∈R,x2-2x+3>0,则命题p的否定是( )
| A、?x∈R,x2-2x+3<0 |
| B、?x∈R,x2-2x+3≤0 |
| C、?x∈R,x2-2x+3<0 |
| D、?x∈R,x2-2x+3≤0 |
在等比数列{an}中,a2=2,a4=6,则a6的值为( )
| A、4 | B、8 | C、18 | D、±18 |
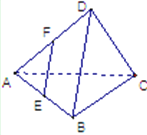 已知空间四面体D-ABC的每条边都等于1,点E,F分别是AB,AD的中点,则
已知空间四面体D-ABC的每条边都等于1,点E,F分别是AB,AD的中点,则| FE |
| DC |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
 如图,质点P在半径为10cm的圆上逆时针作匀速圆周运动,角速度为2rad/s.设A(10,0)为起始点,则时刻t=2时,点P在y轴上的射影点M的速度为
如图,质点P在半径为10cm的圆上逆时针作匀速圆周运动,角速度为2rad/s.设A(10,0)为起始点,则时刻t=2时,点P在y轴上的射影点M的速度为