题目内容
等比数列前三项分别为x，2x+2，3x+3，则第四项为（ ）
A、-
| ||
B、
| ||
| C、4x+4 | ||
| D、（2x+2）÷[（3x+3）x] |
考点：等比数列的前n项和
专题：等差数列与等比数列
分析：由已知条件求出等比数列前三项分别为-4，-6，-9，由此能求出第四项．
解答：
解：∵等比数列前三项分别为x，2x+2，3x+3，
∴（2x+2）2=x（3x+3），
解得x=-4或x=-1（舍），
∴等比数列前三项分别为-4，-6，-9，
∴第四项为-9×(
)=-
．
故选：A．
∴（2x+2）2=x（3x+3），
解得x=-4或x=-1（舍），
∴等比数列前三项分别为-4，-6，-9，
∴第四项为-9×(
| -9 |
| -6 |
| 27 |
| 2 |
故选：A．
点评：本题考查等比数列的第4项的求法，是基础题，解题时要注意等比数列的性质的合理运用．
练习册系列答案
相关题目
已知命题p：?x∈R，x2-2x+3＞0，则命题p的否定是（ ）
| A、?x∈R，x2-2x+3＜0 |
| B、?x∈R，x2-2x+3≤0 |
| C、?x∈R，x2-2x+3＜0 |
| D、?x∈R，x2-2x+3≤0 |
对任意实数a，b定义运算“⊙“：a⊙b=
，设f（x）=（x2-1）⊙（4+x）+k，若函数f（x）的图象与x轴恰有三个交点，则k的取值范围是（ ）
|
| A、[-2，1） |
| B、[0，1] |
| C、（0，1] |
| D、（-2，1） |
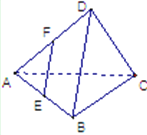已知空间四面体D-ABC的每条边都等于1，点E，F分别是AB，AD的中点，则| FE |
| DC |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
已知函数y=
在三棱锥P-ABC中，△ABC为正三角形，∠PCA=90°，D为PA中点，二面角P-AC-B的大小为为120°，PC=2，AB=2