题目内容
已知ABC-A1B1C1是底面边长为2的正三棱柱,O为BC的中点.
(Ⅰ)设A1O与底面A1B1C1所成的角的大小为α,二面角B-AO-B1的大小为β,
求证:tanβ=
tanα;
(Ⅱ)若点C到平面AB1C1的距离为
,求正三棱柱ABC-A1B1C1的高.
(Ⅰ)设A1O与底面A1B1C1所成的角的大小为α,二面角B-AO-B1的大小为β,
求证:tanβ=
| 3 |
(Ⅱ)若点C到平面AB1C1的距离为
| ||
| 2 |
考点:棱柱、棱锥、棱台的体积,与二面角有关的立体几何综合题
专题:计算题,空间角
分析:(Ⅰ)利用空间线面位置关系作出设A1O与底面A1B1C1所成的角的大小为α与二面角B-AO-B1的大小为β;
(Ⅱ)向量法解决
(Ⅱ)向量法解决
解答:
 解:(Ⅰ)设正三棱柱的高为h,
解:(Ⅰ)设正三棱柱的高为h,
∵AA1⊥平面A1B1C1,平面ABC∥平面A1B1C1,∴A1O与底面A1B1C1所成的角大小等于A1O与底面ABC所成的角大小,即∠AOA1=α,则tanα=
=
,…(2分)
∵AB=AC,O为BC的中点,∴AO⊥BC,
又∵平面BB1C1C⊥平面ABC,交线是BC,AO?平面ABC,∴AO⊥BB1C1C,
∴∠BOB1是二面角B-AO-B1的平面角,即∠BOB1=β,则 tanβ=
=h,…(5分)
∴tanβ=
tanα…(6分)
(Ⅱ) 设O为BC的中点,如图建系,则
=(-
,1,h),
=(0,2,0),
=(1,
,0),…(8分)
设平面AB1C1的一个法向量为
=(x,y,z),则
…(9分)
即
,取
=(h,0,
)…(10分)
∴点C到平面AB1C1的距离为d=|
|=
=
,…(11分)
解得h=1…(12分)
 解:(Ⅰ)设正三棱柱的高为h,
解:(Ⅰ)设正三棱柱的高为h,∵AA1⊥平面A1B1C1,平面ABC∥平面A1B1C1,∴A1O与底面A1B1C1所成的角大小等于A1O与底面ABC所成的角大小,即∠AOA1=α,则tanα=
| AA1 |
| AO |
| h | ||
|
∵AB=AC,O为BC的中点,∴AO⊥BC,
又∵平面BB1C1C⊥平面ABC,交线是BC,AO?平面ABC,∴AO⊥BB1C1C,
∴∠BOB1是二面角B-AO-B1的平面角,即∠BOB1=β,则 tanβ=
| BB1 |
| BO |
∴tanβ=
| 3 |
(Ⅱ) 设O为BC的中点,如图建系,则
| AB1 |
| 3 |
| C1B1 |
| CA |
| 3 |
设平面AB1C1的一个法向量为
| n |
|
即
|
| n |
| 3 |
∴点C到平面AB1C1的距离为d=|
| ||||
|
|
| h | ||
2
|
| ||
| 2 |
解得h=1…(12分)
点评:本题主要考查了正三棱柱中的线面角、二面角的平面角的计算,以及向量法求距离,考查推理论证的能力和表达能力,注意证明过程的严密性.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
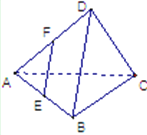 已知空间四面体D-ABC的每条边都等于1,点E,F分别是AB,AD的中点,则
已知空间四面体D-ABC的每条边都等于1,点E,F分别是AB,AD的中点,则| FE |
| DC |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|

 在三棱锥P-ABC中,△ABC为正三角形,∠PCA=90°,D为PA中点,二面角P-AC-B的大小为为120°,PC=2,AB=2
在三棱锥P-ABC中,△ABC为正三角形,∠PCA=90°,D为PA中点,二面角P-AC-B的大小为为120°,PC=2,AB=2 如图,三棱锥A-BCD各棱长都为1,且M、N分别是AB、CD的中点,
如图,三棱锥A-BCD各棱长都为1,且M、N分别是AB、CD的中点,