题目内容
若
<
,则在下列不等式:①a>b;②a<b;③ab(a-b)>0;④ab(a-b)<0中,可以成立的不等式的个数为( )
| 1 |
| a |
| 1 |
| b |
| A、1 | B、2 | C、3 | D、4 |
考点:不等式的基本性质
专题:不等式的解法及应用
分析:①取a=-1,b=2,满足
<
,即可判断出;
②取a=2,b=1,满足
<
,即可判断出;
③由
<
,可得
<0,即ab(b-a)<0,即可判断出;
④由③即可判断出.
| 1 |
| a |
| 1 |
| b |
②取a=2,b=1,满足
| 1 |
| a |
| 1 |
| b |
③由
| 1 |
| a |
| 1 |
| b |
| b-a |
| ab |
④由③即可判断出.
解答:
解:①取a=-1,b=2,满足
<
,则a>b不成立;
②取a=2,b=1,满足
<
,则a<b不成立;
③∵
<
,∴
<0,∴ab(b-a)<0,即ab(a-b)>0,因此正确;
④由③可知:ab(a-b)<0,不正确.
可以成立的不等式的个数只有一个.
故选:A.
| 1 |
| a |
| 1 |
| b |
②取a=2,b=1,满足
| 1 |
| a |
| 1 |
| b |
③∵
| 1 |
| a |
| 1 |
| b |
| b-a |
| ab |
④由③可知:ab(a-b)<0,不正确.
可以成立的不等式的个数只有一个.
故选:A.
点评:本题考查了不等式的基本性质,考查了通过去反例否定一个命题的方法,属于基础题.

练习册系列答案
相关题目
若函数f(x)=x2-2x-4lnx的导函数为f′(x),则f′(x)>0的解集为( )
| A、(0,+∞) |
| B、(-1,0)∪(2,+∞) |
| C、(-1,0) |
| D、(2,+∞) |
已知f(x)=
,则f(f(-2))的值为( )
|
| A、0 | B、2 | C、4 | D、6 |
已知函数f(x)=
,若f(x)≥ax,则a的取值范围是( )
|
| A、(-∞,0] |
| B、(-∞,1] |
| C、[-2,1] |
| D、[-2,0] |
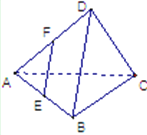 已知空间四面体D-ABC的每条边都等于1,点E,F分别是AB,AD的中点,则
已知空间四面体D-ABC的每条边都等于1,点E,F分别是AB,AD的中点,则| FE |
| DC |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
函数f(x)=x2+1,则f(2)=( )
| A、3 | B、5 | C、7 | D、1 |