题目内容
下面几何体是由（ ）旋转得到的．
A、 |
B、 |
C、 |
D、 |
考点：旋转体（圆柱、圆锥、圆台）
专题：空间位置关系与距离
分析：根据面旋转体的原理即可解，一个三角形绕直角边旋转一周可以得到一个圆锥．一个直角梯形绕着直角边旋转一周得到圆台．
解答：
解：该几体的上部分是圆锥，下部分是圆台，
圆锥的轴截面是直角三角形，
圆台的轴截面是直角梯形，
∴这个几何图形是由直角三角形和直角梯形围绕直角边所在的直线为轴旋转一周得到．
故选：B．
圆锥的轴截面是直角三角形，
圆台的轴截面是直角梯形，
∴这个几何图形是由直角三角形和直角梯形围绕直角边所在的直线为轴旋转一周得到．
故选：B．
点评：本题主要考查空间感知能力，难度不大，学生应注意培养空间想象能力．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
已知x∈[-2，2]、f（x）=2x分别是双曲线f（x）的左、右焦点，f（x）=2为双曲线上的一点，若∠F1PF2=90°，且△F1PF2的三边长成等差数列，则双曲线的离心率是（ ）
| A、2 | B、3 | C、4 | D、5 |
在等比数列{an}中，a2=2，a4=6，则a6的值为（ ）
| A、4 | B、8 | C、18 | D、±18 |
已知f（x）=
，则f（f（-2））的值为（ ）
|
| A、0 | B、2 | C、4 | D、6 |
对任意实数a，b定义运算“⊙“：a⊙b=
，设f（x）=（x2-1）⊙（4+x）+k，若函数f（x）的图象与x轴恰有三个交点，则k的取值范围是（ ）
|
| A、[-2，1） |
| B、[0，1] |
| C、（0，1] |
| D、（-2，1） |
已知函数f（x）=
，若f（x）≥ax，则a的取值范围是（ ）
|
| A、（-∞，0] |
| B、（-∞，1] |
| C、[-2，1] |
| D、[-2，0] |
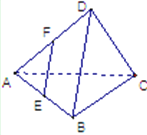已知空间四面体D-ABC的每条边都等于1，点E，F分别是AB，AD的中点，则| FE |
| DC |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
