题目内容
已知F1、F2分别是椭圆C:
+
=1的左、右焦点,点P是椭圆上异于顶点的任意一点,过点F2作直线PF2的垂线交直线x=4于点Q.
(1)当PF1⊥F1F2时,求点Q坐标;
(2)判断直线PQ与直线OP的斜率之积是否为定值?若是,求出定值;若不是,说明理由;
(3)证明:直线PQ与椭圆C只有一个公共点.
| x2 |
| 4 |
| y2 |
| 3 |
(1)当PF1⊥F1F2时,求点Q坐标;
(2)判断直线PQ与直线OP的斜率之积是否为定值?若是,求出定值;若不是,说明理由;
(3)证明:直线PQ与椭圆C只有一个公共点.
考点:直线与圆锥曲线的关系,直线的一般式方程与直线的垂直关系
专题:计算题,作图题,证明题,圆锥曲线中的最值与范围问题
分析:(1)作出图形,由题意可求出点P的坐标,由△PF1F2∽△F2EQ可得点Q(4,4)或(4,-4);
(2)作出图形,设点P(a,b),点Q(4,y),F2(1,0);由PF2⊥QF2可得y=-3
,从而求直线PQ与直线OP的斜率,化简可得kPQ=-
,kOP=
,故kOP×kQP=-
;
(3)由(2)知,直线PQ的方程为:y-b=-
(x-a),与椭圆方程联立化简,借助3a2+4b2=12可将方程简化为3x2-6ax+12-4b2=0,从而求△=(6a)2-4×3(12-4b2)=0,则证明结论.
(2)作出图形,设点P(a,b),点Q(4,y),F2(1,0);由PF2⊥QF2可得y=-3
| a-1 |
| b |
| 3a |
| 4b |
| b |
| a |
| 3 |
| 4 |
(3)由(2)知,直线PQ的方程为:y-b=-
| 3a |
| 4b |
解答:
 解:(1)由题意,作图如右:
解:(1)由题意,作图如右:
由
+
=1可得,y=±
,
则点P(-1,
),
则|PF1|=
,|F1F2|=2;
则由△PF1F2∽△F2EQ知,
=
,
即
=
,
解得,|QE|=4,
则点Q(4,4)或(4,-4);
(2)由题意,如右图:
设点P(a,b),点Q(4,y),F2(1,0);
则由PF2⊥QF2知,
•
=-1,
化简得,y=-3
,
则kPQ=
=
,
又∵
+
=1,
∴b2=3(1-
),
∴kPQ=
=-
,
又∵kOP=
,
∴kOP×kQP=-
,
即直线PQ与直线OP的斜率之积为定值-
.
(3)证明:由题意,直线PQ的方程为:y-b=-
(x-a),
即y=-
x+
a+b=-
x+
,
与
+
=1联立消y,
由
+
=1可化为3a2+4b2=12,
将3a2+4b2=12代入化简可得,
3x2-6ax+12-4b2=0,
则△=(6a)2-4×3(12-4b2)
=12(3a2-12+4b2)=0,
故方程有一个根,
即直线PQ与椭圆C只有一个公共点.
 解:(1)由题意,作图如右:
解:(1)由题意,作图如右:由
| 1 |
| 4 |
| y2 |
| 3 |
| 3 |
| 2 |
则点P(-1,
| 3 |
| 2 |
则|PF1|=
| 3 |
| 2 |
则由△PF1F2∽△F2EQ知,
| |F2E| |
| |PF1| |
| |QE| |
| |F2F1| |
即
| 3 | ||
|
| |QE| |
| 2 |
解得,|QE|=4,
则点Q(4,4)或(4,-4);
(2)由题意,如右图:

设点P(a,b),点Q(4,y),F2(1,0);
则由PF2⊥QF2知,
| b-0 |
| a-1 |
| y-0 |
| 4-1 |
化简得,y=-3
| a-1 |
| b |
则kPQ=
b-(-3
| ||
| a-4 |
| b2+3(a-1) |
| b(a-4) |
又∵
| a2 |
| 4 |
| b2 |
| 3 |
∴b2=3(1-
| a2 |
| 4 |
∴kPQ=
| -3a(a-4) |
| 4b(a-4) |
| 3a |
| 4b |
又∵kOP=
| b |
| a |
∴kOP×kQP=-
| 3 |
| 4 |
即直线PQ与直线OP的斜率之积为定值-
| 3 |
| 4 |
(3)证明:由题意,直线PQ的方程为:y-b=-
| 3a |
| 4b |
即y=-
| 3a |
| 4b |
| 3a |
| 4b |
| 3a |
| 4b |
| 3 |
| b |
与
| x2 |
| 4 |
| y2 |
| 3 |
由
| a2 |
| 4 |
| b2 |
| 3 |
将3a2+4b2=12代入化简可得,
3x2-6ax+12-4b2=0,
则△=(6a)2-4×3(12-4b2)
=12(3a2-12+4b2)=0,
故方程有一个根,
即直线PQ与椭圆C只有一个公共点.
点评:本题考查了圆锥曲线与直线的位置关系,利用到了三角形的相似比,线线垂直的特征及直线的斜率的求法等,化简非常难,注意要细心,属于难题.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
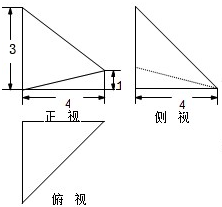 已知一个几何体的三视图如图所示,其中正视图是直角梯形.
已知一个几何体的三视图如图所示,其中正视图是直角梯形.