题目内容
已知全集U=R，集合A={x|a≤x≤b}，集合B={x|x2-x-2＞0}，若A∩B=φ，A∪B=U，则a，b的值分别是（ ）
| A、-1，2 | B、2，-1 |
| C、-1，1 | D、-2，2 |
考点：交集及其运算
专题：集合
分析：求解一元二次不等式化简结合B，然后由A∩B=φ，A∪B=U求得a，b的值．
解答：
解：由x2-x-2＞0，得x＜-1或x＞2，
∴B={x|x2-x-2＞0}={x|x＜-1或x＞2}，
又∵A={x|a≤x≤b}，且A∩B=∅，A∪B=U，
∴a=-1，b=2．
故选：A．
∴B={x|x2-x-2＞0}={x|x＜-1或x＞2}，
又∵A={x|a≤x≤b}，且A∩B=∅，A∪B=U，
∴a=-1，b=2．
故选：A．
点评：本题考查了交集及其运算，考查了一元二次不等式的解法，是基础题．
练习册系列答案
相关题目
将函数f（x）=sin（x-
）图象上所有点的横坐标缩短到原来的一半（纵坐标不变），再将它的图象向左平移φ个单位（φ＞0），得到了一个偶函数的图象，则φ的最小值为（ ）
| π |
| 6 |
A、
| ||
B、
| ||
C、
| ||
D、
|
复数z1=3+i，z2满足z1•z2=4-2i（i为虚数单位），则z2在复平面内对应的点在（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
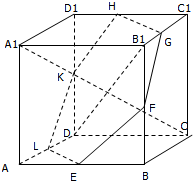如图所示，正方体ABCD-A1B1C1D1中，E、F、G、H、K、L分别为AB、BB1、B1C1、C1D1、D1D、DA的中点，求证：A1C⊥平面EFGHKL．