题目内容
若函数f(x)为定义在R上的奇函数,且在(0,+∞)内是增函数,又f(2)=0,则不等式xf(x)<0的解集为 .
考点:奇偶性与单调性的综合
专题:函数的性质及应用
分析:易判断f(x)在(-∞,0)上的单调性及f(x)图象所过特殊点,作出f(x)的草图,根据图象可解不等式.
解答:
解:∵f(x)在R上是奇函数,且f(x)在(0,+∞)上是增函数,
∴f(x)在(-∞,0)上也是增函数,
由f(2)=0,得f(-2)=-f(2)=0,
即f(-2)=0,
由f(-0)=-f(0),得f(0)=0,
作出f(x)的草图,如图所示:
由图象,得xf(x)<0?
或
,
解得0<x<2或-2<x<0,
∴xf(x)<0的解集为:(-2,0)∪(0,2),
故答案为:(-2,0)∪(0,2)
∴f(x)在(-∞,0)上也是增函数,
由f(2)=0,得f(-2)=-f(2)=0,

即f(-2)=0,
由f(-0)=-f(0),得f(0)=0,
作出f(x)的草图,如图所示:
由图象,得xf(x)<0?
|
|
解得0<x<2或-2<x<0,
∴xf(x)<0的解集为:(-2,0)∪(0,2),
故答案为:(-2,0)∪(0,2)
点评:本题考查函数奇偶性、单调性的综合应用,考查数形结合思想,灵活作出函数的草图是解题关键.

练习册系列答案
相关题目
p:若x2+y2≠0,则x,y不全为零,q:若m>-2,则x2+2x-m=0有实根,则( )
| A、“p∨q”为真 |
| B、“¬p”为真 |
| C、“p∧q”为真 |
| D、“¬q”为假 |
已知正项等比数列{an}满足a7=a6+2a5.若存在两项am,an使得
=4a1,则
+
的最小值为( )
| aman |
| 1 |
| m |
| 9 |
| n |
A、
| ||
B、
| ||
C、
| ||
D、
|
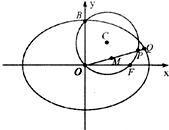 已知圆C经(x-1)2+(y-2)2=5经过椭圆E:
已知圆C经(x-1)2+(y-2)2=5经过椭圆E: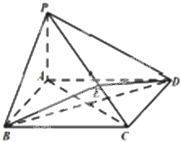 如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE.PA=1,AD=2.
如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE.PA=1,AD=2.