题目内容
下列运用基本不等式求最值,使用正确的个数是( )
①已知ab≠0,求
+
的最小值;解答过程:
+
≥2
=2.
②求函数y=
的最小值;解答过程:可化得y=
+
≥2
③设x>1,求y=x+
的最小值;解答过程:y=x+
≥2
,当且仅当x=
即x=2时等号成立,把x=2代入2
得最小值为4.
①已知ab≠0,求
| a |
| b |
| b |
| a |
| a |
| b |
| b |
| a |
|
②求函数y=
| x2+5 | ||
|
| x2+4 |
| 1 | ||
|
③设x>1,求y=x+
| 2 |
| x-1 |
| 2 |
| x-1 |
|
| 2 |
| x-1 |
|
| A、0个 | B、1个 | C、2个 | D、3个 |
考点:命题的真假判断与应用
专题:不等式的解法及应用
分析:利用基本不等式成立的条件,对三个求解过程分别进行判断即可得到答案.
解答:
解:基本不等式适用于两个正数,当ab<0,
与
均为负值,此时
+
=-[(-
)+(-
)]≤2
=-2,故①的用法有误;
y=
+
≥2,当且仅当
=
,即
=1时取等号,但
≥2,故②的用法有误;
y=x+
=y=x-1+
+1≥2
+1,当且仅当x-1=
,即x=
+1时取等号,故③的用法有误;
故使用正确的个数是0个,
故选:A
| a |
| b |
| b |
| a |
| a |
| b |
| b |
| a |
| a |
| b |
| b |
| a |
(-
|
y=
| x2+4 |
| 1 | ||
|
| x2+4 |
| 1 | ||
|
| x2+4 |
| x2+4 |
y=x+
| 2 |
| x-1 |
| 2 |
| x-1 |
| 2 |
| 2 |
| 2 |
故使用正确的个数是0个,
故选:A
点评:本题主要考查基本不等式的应用,注意基本不等式成立的三个基本条件:一正,二定,三相等,缺一不可.

练习册系列答案
相关题目
| a |
| b |
| a |
| b |
| A、(5,7) |
| B、(5,9) |
| C、(3,7) |
| D、(3,9) |
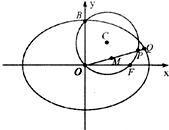 已知圆C经(x-1)2+(y-2)2=5经过椭圆E:
已知圆C经(x-1)2+(y-2)2=5经过椭圆E: