题目内容
已知sinα=
,α∈(
,π).
(1)求cosα,tanα的值;
(2)求cos2α的值;
(3)求sin(α+
)的值.
| 4 |
| 5 |
| π |
| 2 |
(1)求cosα,tanα的值;
(2)求cos2α的值;
(3)求sin(α+
| π |
| 6 |
考点:同角三角函数基本关系的运用
专题:计算题,三角函数的求值
分析:(1)利用同角三角函数基本关系,求cosα,tanα的值;
(2)利用cos2α=2cos2α-1,求cos2α的值;
(3)利用sin(α+
)=
sinα+
cosα,求sin(α+
)的值.
(2)利用cos2α=2cos2α-1,求cos2α的值;
(3)利用sin(α+
| π |
| 6 |
| ||
| 2 |
| 1 |
| 2 |
| π |
| 6 |
解答:
解:∵sinα=
,α∈(
,π),∴
(1)cosα=-
,tanα=-
;
(2)cos2α=2cos2α-1=2×
-1=-
;
(3)sin(α+
)=
sinα+
cosα=
×
+
×(-
)=
.
| 4 |
| 5 |
| π |
| 2 |
(1)cosα=-
| 3 |
| 5 |
| 4 |
| 3 |
(2)cos2α=2cos2α-1=2×
| 9 |
| 25 |
| 7 |
| 25 |
(3)sin(α+
| π |
| 6 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 4 |
| 5 |
| 1 |
| 2 |
| 3 |
| 5 |
4
| ||
| 10 |
点评:本题考查同角三角函数基本关系的运用,考查二倍角公式,考查学生的计算能力,正确运用公式是关键.

练习册系列答案
相关题目
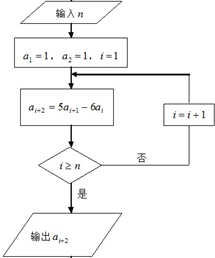 已知数列{an}满足如图所示的程序框图.
已知数列{an}满足如图所示的程序框图.