Question

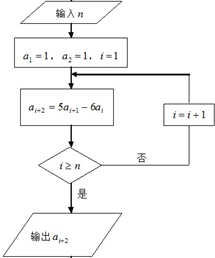已知数列{a_n}满足如图所示的程序框图．
（1）写出数列{a_n}的一个递推关系式；
（2）证明：{a_n+1-3a_n}是等比数列，并求{a_n}的通项公式；
（3）求数列{n（a_n+3^n-1）}-的前n项和T_n．

Answer 1

考点：数列的求和,数列递推式,程序框图

专题：等差数列与等比数列

分析：（1）由程序框图可知，a₁=a₂=1，a_n+2=5a_n+1-6a_n．
（2）由a_n+2=5a_n+1-6a_n可得a_n+2-3a_n+1=2（a_n+1-3a_n），且a₂-3a₁=-2．利用等比数列的通项公式可得an+1-3an=-2n，化为

an+1

2n+1

-1=

3

2

(

an

2n

-1)，再一次利用等比数列的通项公式即可得出．
（3）利用“错位相减法”、等比数列的前n项和公式即可得出．

解答： 解：（1）由程序框图可知，a₁=a₂=1，a_n+2=5a_n+1-6a_n．
（2）由a_n+2=5a_n+1-6a_n可得a_n+2-3a_n+1=2（a_n+1-3a_n），且a₂-3a₁=-2．
可知，数列{a_n+1-3a_n}是以-2为首项，2为公比的等比数列，
可得an+1-3an=-2n，化为

an+1

2n+1

-1=

3

2

(

an

2n

-1)，又

a1

2

-1=-

1

2

，
∴数列{

an

2n

-1}是以-

1

2

为首项，

3

2

为公比的等比数列，

an

2n

-1=-

1

2

×(

3

2

)n-1，可得an=2n-3n-1．
（3）n（a_n+3^n-1）=n•2ⁿ，
则T_n=2+2×2²+3×2³+…+n×2ⁿ，
∴2T_n=2²+2×2³+3×2⁴+…+（n-1）×2ⁿ+n×2ⁿ⁺¹，
∴-T_n=2+2²+2³+…+2ⁿ-n×2ⁿ⁺¹=

2(2n-1)

2-1

-n•2ⁿ⁺¹=（1-n）•2ⁿ⁺¹-2，
∴Tn=(n-1)2n+1+2．

点评：本题考查了“错位相减法”、等比数列的通项公式及其前n项和公式、程序框图，考查了变形与转化能力，考查了推理能力与计算能力，属于难题．