题目内容

O（0，0，0）、A（
3
，0，0）、B（0，1，0）、C（-
3
，0，0）、F（0，0，
3
）   向量
CF
=
 
，
CB
=
 
、∠BFC=
 
，∠AFC=
 
．
考点：空间向量的夹角与距离求解公式
专题：空间向量及应用
分析：利用向量坐标运算、向量夹角公式即可得出．
解答： 解：
CF
=(
3
，0，
3
)，
CB
=(
3
，1，0)，
FC
=(-
3
，0，-
3
)，
FB
=(0，1，-
3
)，
FA
=(
3
，0，-
3
)．
∴cos∠BFC=
FB
•
FC
|
FB
||
FC
|
=
3
6
×2
=
6
4
．
∴∠BFC=arccos
6
4
．
∵cos∠AFC=
FA
•
FC
|
FA
||
FC
|
=0，
∴∠AFC=
π
2
．
故答案分别为：(
3
，0，
3
)，(
3
，1，0)，arccos
6
4
，
π
2
．
点评：本题考查了向量坐标运算、向量夹角公式、数量积运算，考查了计算能力，属于基础题．
练习册系列答案
相关题目
已知函数f（x）=x2-2x+a（x∈[0，3]），它的任意三个函数值总可以作为一个三角形的三边长，则a的取值范围是
 
．
已知sinα=
4
5
，α∈（
π
2
，π）．
（1）求cosα，tanα的值；
（2）求cos2α的值；
（3）求sin（α+
π
6
）的值．
（
2
-1）-1．
若
a
=（2，-3，5），
b
=（-3，1，-4），求
a
+
b
，6
a
，
a
•
b
，|
a
-2
b
|．
在极坐标系中，已知点P（2，
3π
2
），曲线C：p=4cosθ．以极点为原点，极轴为x轴的正半轴建立平面直角坐标系，过点P作倾斜角为α的直线l．
（1）写出直线l的参数方程和曲线C的普通方程；
（2）若直线l交曲线C于点M，N两点，求|PM|2+|PN|2的最大值及其相应α的值．
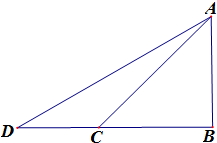如图，塔AB底部为点B，若C，D两点相距为100m并且与点B在同一水平线上，现从C，D两点测得塔顶A的仰角分别为45°和30°，则塔AB的高约为（精确到0.1m，
3
≈1.73，
2
≈1.41）（　　）
A、36.5B、115.6
C、120.5D、136.5
二项式（x2+
1
x
）5的展开式中，x的系数为（　　）
A、10B、15C、20D、25
已知命题p：3≥3，q：3＞4，则下列判断正确的是（　　）
A、p∨q为真，p∧q为真，￢p为假
B、p∨q为真，p∧q为假，￢p为真
C、p∨q为假，p∧q为假，￢p为假
D、p∨q为真，p∧q为假，￢p为假

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网