题目内容
已知递增的等比数列{an}的前n项和为Sn,a5=32,a3、a4的等差中项为3a2.
(1)求an的通项公式;
(2)设bn=
,求数列bn的前n项和Tn.
(1)求an的通项公式;
(2)设bn=
| n |
| a2n-1 |
考点:数列的求和,等比数列的通项公式
专题:等差数列与等比数列
分析:(1)根据等比数列的通项公式、等差中项的性质,列出关于a1、q的方程,求出a1、q的值,代入an化简;
(2)由(1)和题意化简bn,再利用错位相减法求出数列bn的前n项和Tn.
(2)由(1)和题意化简bn,再利用错位相减法求出数列bn的前n项和Tn.
解答:
解:(1)设递增等比数列{an}首项、公比为a1、q,且q>0,
因为a5=32,a3、a4的等差中项为3a2,
所以
,解得a1=2、q=2,
则an=2•2n-1=2n;
(2)由(1)得,bn=
=
,
所以Tn=
+
+
+…+
,①
Tn=
+
+
+…+
,②
①-②得
Tn=
+
+
+…+
-
=
-
=
-(
+
)•
,
则Tn=
-
•
.
因为a5=32,a3、a4的等差中项为3a2,
所以
|
则an=2•2n-1=2n;
(2)由(1)得,bn=
| n |
| a2n-1 |
| n |
| 22n-1 |
所以Tn=
| 1 |
| 21 |
| 2 |
| 23 |
| 3 |
| 25 |
| n |
| 22n-1 |
| 1 |
| 4 |
| 1 |
| 23 |
| 2 |
| 25 |
| 3 |
| 27 |
| n |
| 22n+1 |
①-②得
| 3 |
| 4 |
| 1 |
| 21 |
| 1 |
| 23 |
| 1 |
| 25 |
| 1 |
| 22n-1 |
| n |
| 22n+1 |
=
| ||||
1-
|
| n |
| 22n+1 |
| 2 |
| 3 |
| 2 |
| 3 |
| n |
| 2 |
| 1 |
| 22n |
则Tn=
| 8 |
| 9 |
| 3n+4 |
| 9 |
| 1 |
| 22n-1 |
点评:本题考查等比数列的通项公式、前n项和公式,错位相减法求数列的前n项和,以及方程思想,考查化简能力.

练习册系列答案
相关题目
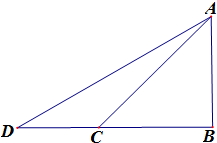 如图,塔AB底部为点B,若C,D两点相距为100m并且与点B在同一水平线上,现从C,D两点测得塔顶A的仰角分别为45°和30°,则塔AB的高约为(精确到0.1m,
如图,塔AB底部为点B,若C,D两点相距为100m并且与点B在同一水平线上,现从C,D两点测得塔顶A的仰角分别为45°和30°,则塔AB的高约为(精确到0.1m,| 3 |
| 2 |
| A、36.5 | B、115.6 |
| C、120.5 | D、136.5 |
给定两个命题p,q,若¬p是q的必要而不充分条件,则p是¬q的( )
| A、必要而不充分条件 |
| B、充分而不必要条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |