题目内容
1.已知函数$f(x)=\left\{{\begin{array}{l}{{2^x}-1,x≤1}\\{1+{{log}_2}x,x>1}\end{array}}\right.$,则函数f(x)的零点是( )| A. | x=0或$x=\frac{1}{2}$ | B. | x=-2或x=0 | C. | $x=\frac{1}{2}$ | D. | x=0 |
分析 利用分段函数,分别求出零点,即可得出结论.
解答 解:由题意,x≤1,f(x)=2x-1=0,x=0,成立;
x>1,f(x)=1+log2x=0,x=$\frac{1}{2}$,不成立,
故选D.
点评 本题考查函数的零点,考查分段函数,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
11.已知F1、F2为双曲线的焦点,过F2垂直于实轴的直线交双曲线于A、B两点,BF1交y轴于点C,若AC⊥BF1,则双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
13.如图所示程序框图,执行该程序后输出的结果是$\frac{29}{10}$,则判断框内应填入的条件是( )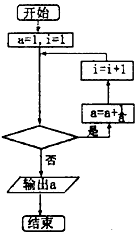

| A. | i>47 | B. | i≥4? | C. | i<4? | D. | i≤4? |
4.$f(x)=\sqrt{2}sin({x+φ})-a+{e^{-x}}$,$φ∈({0,\frac{π}{2}})$,已知f(x)的图象在(0,f(0))处的切线与x轴平行或重合.
(1)求φ的值;
(2)若对?x≥0,f(x)≤0恒成立,求a的取值范围;
(3)利用如表数据证明:$\sum_{k=1}^{157}{sin\frac{kπ}{314}<106}$.
(1)求φ的值;
(2)若对?x≥0,f(x)≤0恒成立,求a的取值范围;
(3)利用如表数据证明:$\sum_{k=1}^{157}{sin\frac{kπ}{314}<106}$.
| ${e^{\frac{π}{314}}}$ | ${e^{-\frac{π}{314}}}$ | ${e^{\frac{78π}{314}}}$ | ${e^{-\frac{78π}{314}}}$ | ${e^{\frac{79π}{314}}}$ | ${e^{-\frac{79π}{314}}}$ |
| 1.010 | 0.990 | 2.182 | 0.458 | 2.204 | 0.454 |
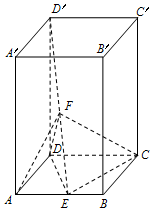 如图,底面为平行四边形的四棱柱ABCD-A'B'C'D'中,DD'⊥平面ABCD,∠DAB=$\frac{π}{3}$,AB=2AD,DD'=3AD,E、F分别是线段AB、D'E的中点.
如图,底面为平行四边形的四棱柱ABCD-A'B'C'D'中,DD'⊥平面ABCD,∠DAB=$\frac{π}{3}$,AB=2AD,DD'=3AD,E、F分别是线段AB、D'E的中点.