题目内容
6.已知等差数列{an}中,a2=6,a5=12.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设${b_n}=\frac{4}{{{a_n}•{a_{n+1}}}}$,求数列{bn}的前n项和Sn的值.
分析 (1)利用等差数列的通项公式即可得出.
(2)利用“裂项求和”方法即可得出.
解答 解:设{an}的首项为a1,公差为d,则由a2=6,a5=12,得3d=a5-a2=6,解得d=2.
∴a1=a2-d=6-2=4,
∴an=a1+(n-1)d=4+2(n-1)=2n+2,
即数列{an}的通项公式为an=2n+2.
(Ⅱ)依题意有${b_n}=\frac{4}{{{a_n}•{a_{n+1}}}}=\frac{4}{(2n+2)•[2(n+1)+2]}=\frac{1}{(n+1)(n+2)}=\frac{1}{n+1}-\frac{1}{n+2}$,
∴${S_n}={b_1}+{b_2}+…+{b_n}=(\frac{1}{2}-\frac{1}{3})+(\frac{1}{3}-\frac{1}{4})+…+(\frac{1}{n+1}+\frac{1}{n+2})$=$\frac{1}{2}-\frac{1}{n+2}=\frac{n}{2n+4}$.
点评 本题考查了等差数列的通项公式、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
14.设函数$f(x)=\frac{{6sinxcosx-4cosx{{sin}^3}x}}{{2\sqrt{2}+sin(2x+\frac{π}{4})+cos(2x+\frac{π}{4})}}$,则( )
| A. | y=f(x)是偶函数,在$(0,\frac{π}{2})$上单调递增 | B. | y=f(x)是奇函数,在$(0,\frac{π}{4})$上单调递增 | ||
| C. | y=f(x)是偶函数,在$(0,\frac{π}{2})$上单调递减 | D. | y=f(x)是奇函数,在$(0,\frac{π}{4})$上单调递减 |
1.已知函数$f(x)=\left\{{\begin{array}{l}{{2^x}-1,x≤1}\\{1+{{log}_2}x,x>1}\end{array}}\right.$,则函数f(x)的零点是( )
| A. | x=0或$x=\frac{1}{2}$ | B. | x=-2或x=0 | C. | $x=\frac{1}{2}$ | D. | x=0 |
15.若${(a+i)^2}-\frac{1}{i}∈R(a∈R,i$是虚数单位),则a=( )
| A. | 1 | B. | 0 | C. | 一$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
9.已知集合A={0,1,2},B={1,m},若A∩B=B,则实数m的取值集合是( )
| A. | {0} | B. | {2} | C. | {0,2} | D. | {0,1,2} |
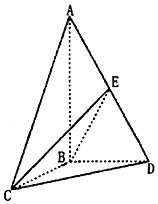 如图,三棱锥A-BCD中,AB⊥平面BCD,AC=AD=2,BC=BD=1,点E是线段AD的中点.
如图,三棱锥A-BCD中,AB⊥平面BCD,AC=AD=2,BC=BD=1,点E是线段AD的中点.