题目内容
15.已知一条直线经过点P(2,1),且与圆x2+y2=10相交,截得的弦长为2$\sqrt{5}$,求这条直线的方程.分析 分两种情况进行讨论,斜率存在和不存在;当斜率不存在时直线方程为x=2,进行验证可得结论,过点P(2,1)的直线l,当斜率存在时,直线方程被圆x2+y2=10截得的弦长要为2 $\sqrt{5}$,利用垂径定理,只要满足圆心(0,0)到直线的距离为 $\sqrt{5}$即可,从而求出斜率k.
解答 解:过点P(2,1)的直线l,当斜率不存在时直线方程为x=2,
这时验证,被圆x2+y2=10截得的弦长显然不为为2$\sqrt{5}$.这不合题意.
过点P(2,1)的直线l,当斜率存在时,直线方程为y=k(x-2)+1,
这时,被圆x2+y2=10截得的弦长要为2$\sqrt{5}$,只要满足圆心(0,0)到直线的距离为$\sqrt{5}$即可.
即有等式为$\frac{|-2k+1|}{\sqrt{1+{k}^{2}}}$=$\sqrt{5}$.
解得k=-2,
故所求的直线方程为:2x+y-5=0.
点评 本题考查直线与圆的位置关系,考查计算能力,解决直线与圆的问题,要充分利用圆的几何性质,数形结合加以解决.

练习册系列答案
相关题目
10.若sinα+cosα=-$\frac{7}{5}$,则角α是( )
| A. | 第一象限角 | B. | 第二象限角 | C. | 第三象限角 | D. | 第四象限角 |
7.下列命题中,正确的个数为( )
(1)函数y=$\frac{1}{{a}^{x}}$(a>0,a≠1)不是指数函数
(2)指数函数不具有奇偶性
(3)指数函数在其定义域上是单调函数.
(1)函数y=$\frac{1}{{a}^{x}}$(a>0,a≠1)不是指数函数
(2)指数函数不具有奇偶性
(3)指数函数在其定义域上是单调函数.
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
5.在△ABC中,若角A、B、C 的对边分别为a,b,c,且atanB=5,bsinA=4,则a等于( )
| A. | $\frac{15}{4}$ | B. | $\frac{25}{4}$ | C. | 5 | D. | $\frac{20}{3}$ |
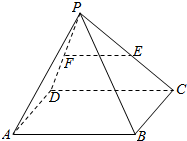 如图所示,P是平行四边形ABCD外一点,E,F分别是PC,PD的中点,判断EF与平面PAB是否平行?
如图所示,P是平行四边形ABCD外一点,E,F分别是PC,PD的中点,判断EF与平面PAB是否平行?