题目内容
13.在△ABC中,$\frac{cosA}{cosB}$=$\frac{b}{a}$=$\frac{5}{3}$,则△ABC的形状是怎样?分析 先由正弦定理和二倍角公式,得到sin2A=sin2B,再根据边角关系得到A+B=$\frac{π}{2}$,问题得以判断.
解答 解:由正弦定理可得$\frac{b}{a}$=$\frac{sinB}{sinA}$,
∵$\frac{cosA}{cosB}$=$\frac{b}{a}$=$\frac{5}{3}$,
∴$\frac{cosA}{cosB}$=$\frac{sinB}{sinA}$,
∴cosAsinA=sinBcosB,
∴$\frac{1}{2}$sin2A=$\frac{1}{2}$sin2B,
∴sin2A=sin2B,
∵$\frac{b}{a}$=$\frac{5}{3}$,
∴π-2A=2B,
∴A+B=$\frac{π}{2}$,
∴△ABC是直角三角形
点评 本题考查了正弦定理的应用以及三角函数的化简,以及三角的边角的关系,属于中档题.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
5.在△ABC中,若角A、B、C 的对边分别为a,b,c,且atanB=5,bsinA=4,则a等于( )
| A. | $\frac{15}{4}$ | B. | $\frac{25}{4}$ | C. | 5 | D. | $\frac{20}{3}$ |
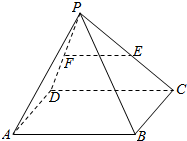 如图所示,P是平行四边形ABCD外一点,E,F分别是PC,PD的中点,判断EF与平面PAB是否平行?
如图所示,P是平行四边形ABCD外一点,E,F分别是PC,PD的中点,判断EF与平面PAB是否平行?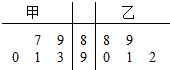 甲、乙两名学生五次数学测验成绩(百分制)如图所示.
甲、乙两名学生五次数学测验成绩(百分制)如图所示.