题目内容
20.某三棱锥的三视图如图所示,则该三棱锥的表面积是( )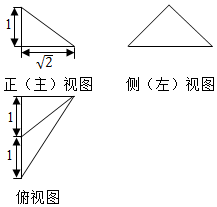
| A. | 2+2$\sqrt{2}$ | B. | 2+$\sqrt{2}$ | C. | 4+2$\sqrt{2}$ | D. | 4+$\sqrt{2}$ |
分析 根据三视图作出棱锥直观图,根据棱锥的结构特征计算每个侧面的面积.
解答 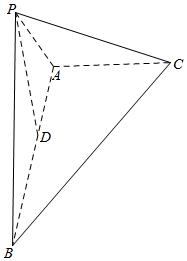 解:根据三视图作出三棱锥P-ABC的直观图,
解:根据三视图作出三棱锥P-ABC的直观图,
P在底面ABC中的射影为AB的中点D,AB⊥AC,PD=1,AB=2,AC=$\sqrt{2}$.
∴S△PAB=$\frac{1}{2}AB•PD$=$\frac{1}{2}×2×1$=1.S△ABC=$\frac{1}{2}AB•AC$=$\frac{1}{2}×2×\sqrt{2}$=$\sqrt{2}$.
由PD⊥平面ABC得PD⊥AC,故而AC⊥平面PAD.∴AC⊥PA.
∵PA=$\sqrt{P{D}^{2}+A{D}^{2}}$=$\sqrt{2}$,∴S△PAC=$\frac{1}{2}PA•AC$=$\frac{1}{2}×\sqrt{2}×\sqrt{2}$=1.
由勾股定理得PB=$\sqrt{P{D}^{2}+B{D}^{2}}$=$\sqrt{2}$,PC=$\sqrt{P{A}^{2}+A{C}^{2}}$=2,BC=$\sqrt{A{B}^{2}+A{C}^{2}}$=$\sqrt{6}$,
∴PB2+PC2=BC2,∴PB⊥PC.
∴S△PBC=$\frac{1}{2}PB•PC$=$\frac{1}{2}×\sqrt{2}×2$=$\sqrt{2}$.
∴三棱锥额表面积S=1+$\sqrt{2}$+1+$\sqrt{2}$=2+2$\sqrt{2}$.
故选A.
点评 本题考查了棱锥的结构特征和三视图,多面体的表面积计算,属于中档题.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
5.在△ABC中,若角A、B、C 的对边分别为a,b,c,且atanB=5,bsinA=4,则a等于( )
| A. | $\frac{15}{4}$ | B. | $\frac{25}{4}$ | C. | 5 | D. | $\frac{20}{3}$ |
11.原点O(0,0)与点A(-4,2)关于直线l对称,则直线l的方程是( )
| A. | x+2y=0 | B. | 2x-y+5=0 | C. | 2x+y+3=0 | D. | x-2y+4=0 |
8.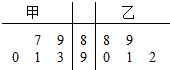 甲、乙两名学生五次数学测验成绩(百分制)如图所示.
甲、乙两名学生五次数学测验成绩(百分制)如图所示.
①甲同学成绩的中位数大于乙同学成绩的中位数;
②甲同学的平均分与乙同学的平均分相等;
③甲同学成绩的方差大于乙同学成绩的方差.
以上说法正确的是( )
 甲、乙两名学生五次数学测验成绩(百分制)如图所示.
甲、乙两名学生五次数学测验成绩(百分制)如图所示.①甲同学成绩的中位数大于乙同学成绩的中位数;
②甲同学的平均分与乙同学的平均分相等;
③甲同学成绩的方差大于乙同学成绩的方差.
以上说法正确的是( )
| A. | ①② | B. | ②③ | C. | ①③ | D. | ①②③ |
15.已知平面α和直线a,b,若a∥α,则“b⊥a”是“b⊥α”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
5.已知集合A={-1,0,1,2},B={x|x<2},则A∩B=( )
| A. | {-1,0,1} | B. | {-1,0,2} | C. | {-1,0} | D. | {0,1} |
12.向顶角为120°的等腰三角形ABC(其中AC=BC)内任意投一点M,则AM小于AC的概率为( )
| A. | $\frac{{\sqrt{3}π}}{3}$ | B. | $\frac{{\sqrt{3}π}}{9}$ | C. | $\frac{1}{2}$ | D. | $\frac{π}{3}$ |