题目内容
函数y=sinx在区间[
,
]上的值域是 .
| π |
| 3 |
| 2π |
| 3 |
考点:正弦函数的图象
专题:三角函数的图像与性质
分析:直接利用定义域,根据函数的单调性求函数的值域求函数的值域.
解答:
解:由于x∈[
,
],
根据正弦函数的单调性,
所以:
≤sinx≤1,
即函数的值域为:[
,1],
故答案为:[
,1]
| π |
| 3 |
| 2π |
| 3 |
根据正弦函数的单调性,
所以:
| ||
| 2 |
即函数的值域为:[
| ||
| 2 |
故答案为:[
| ||
| 2 |
点评:本题考查的知识要点:利用定义域求正弦函数的值域.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
在△ABC中,“sinA>
”是“A>
”的( )
| ||
| 2 |
| π |
| 3 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
函数y=x2-2x+3在区间[-1,2]上的值域为( )
| A、[2,3] |
| B、[3,6] |
| C、[2,6] |
| D、[2,+∞) |
点P(2,-1)到直线4x+3y+10=0的距离是( )
A、
| ||
B、
| ||
| C、3 | ||
| D、4 |
抛物线y2=4x上与焦点相距最近的点的坐标是( )
| A、(0,0) |
| B、(1,2) |
| C、(1,-2) |
| D、以上都不是 |
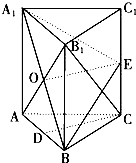 如图三棱柱ABC-A1B1C1中,每个侧面都是正方形,D为底边AB中点,E为侧棱CC1中点,AB1与A1B交于点O.
如图三棱柱ABC-A1B1C1中,每个侧面都是正方形,D为底边AB中点,E为侧棱CC1中点,AB1与A1B交于点O.