题目内容
设a≥0,f(x)=x-1-ln2x+2alnx(x>0).
(Ⅰ)令F(x)=xf′(x),讨论F(x)在(0,+∞)内的单调性并求极值;
(Ⅱ)当x>1时,试判断
与lnx-2a的大小.
(Ⅰ)令F(x)=xf′(x),讨论F(x)在(0,+∞)内的单调性并求极值;
(Ⅱ)当x>1时,试判断
| x-1 |
| lnx |
考点:利用导数研究函数的单调性,利用导数研究函数的极值
专题:导数的综合应用
分析:(Ⅰ)根据求导法则有f′(x)=1-
+
,(x>0),得F(x)=xf′(x)=x-2lnx+2a,x>0,于是F′x)=
,x>0,从而在x=2处取得极小值F(2)=2-ln2+2a,函数无极大值.
(Ⅱ)由a≥0知,F(x)的极小值F(2)=2-2ln2+2a>0.从而当x>0时,恒有f′(x)>0,故f(x)在(0,+∞)内单调增加.所以当x>1时,f(x)>f(1)=0,即x-1-ln2x+2alnx>0.故当x>1时,恒有x-1>ln2x-2alnx.又lnx>0.所以
>lnx-2a.
| 2lnx |
| x |
| 2a |
| x |
| x-2 |
| x |
(Ⅱ)由a≥0知,F(x)的极小值F(2)=2-2ln2+2a>0.从而当x>0时,恒有f′(x)>0,故f(x)在(0,+∞)内单调增加.所以当x>1时,f(x)>f(1)=0,即x-1-ln2x+2alnx>0.故当x>1时,恒有x-1>ln2x-2alnx.又lnx>0.所以
| x-1 |
| lnx |
解答:
(Ⅰ)解:根据求导法则有f′(x)=1-
+
,(x>0),
故F(x)=xf′(x)=x-2lnx+2a,x>0,
于是F′x)=
,x>0,
列表如下:
故知F(x)在(0,2)内是减函数,在(2,+∞)内是增函数,
所以,在x=2处取得极小值F(2)=2-ln2+2a,函数无极大值.
(Ⅱ)由a≥0知,F(x)的极小值F(2)=2-2ln2+2a>0.
于是由上表知,对一切x∈(0,+∞),恒有F(x)=xf′(x)>0.
从而当x>0时,恒有f′(x)>0,故f(x)在(0,+∞)内单调增加.
所以当x>1时,f(x)>f(1)=0,即x-1-ln2x+2alnx>0.
故当x>1时,恒有x-1>ln2x-2alnx.又lnx>0.
所以
>lnx-2a.
| 2lnx |
| x |
| 2a |
| x |
故F(x)=xf′(x)=x-2lnx+2a,x>0,
于是F′x)=
| x-2 |
| x |
列表如下:
| x | (0,2) | 2 | (2,+∞) |
| F′(x) | - | 0 | + |
| F(x) | ↓ | 极小值F(2) | ↑ |
所以,在x=2处取得极小值F(2)=2-ln2+2a,函数无极大值.
(Ⅱ)由a≥0知,F(x)的极小值F(2)=2-2ln2+2a>0.
于是由上表知,对一切x∈(0,+∞),恒有F(x)=xf′(x)>0.
从而当x>0时,恒有f′(x)>0,故f(x)在(0,+∞)内单调增加.
所以当x>1时,f(x)>f(1)=0,即x-1-ln2x+2alnx>0.
故当x>1时,恒有x-1>ln2x-2alnx.又lnx>0.
所以
| x-1 |
| lnx |
点评:本题考察了函数的单调性,函数的极值问题,导数的应用,是一道综合题.

练习册系列答案
相关题目
等差数列{an}的公差d<0,且a32=a112,则该数列的前n项和取得最大值时,n=( )
| A、6 | B、7 | C、6或7 | D、7或8 |
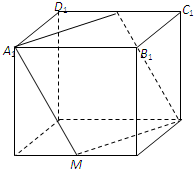 在棱长为a的正方体ABCD-A1B1C1D1中,M是棱AB的中点,过A1,M,C三点的平面交棱C1D1于N点,
在棱长为a的正方体ABCD-A1B1C1D1中,M是棱AB的中点,过A1,M,C三点的平面交棱C1D1于N点,