题目内容
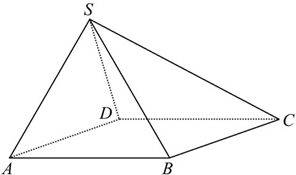 (能力挑战题)如图,已知四棱锥S-ABCD的底面ABCD是菱形,∠BAD=60°,且SA=SB=SD=AB=2.
(能力挑战题)如图,已知四棱锥S-ABCD的底面ABCD是菱形,∠BAD=60°,且SA=SB=SD=AB=2.(1)求证:AB⊥SD.
(2)求S到底面ABCD的距离.
(3)设G为CD的中点,在线段SA上是否存在一点F,使得GF∥平面SBC?
(4)在线段AB上是否存在一点P,使得SP与平面SCD所成的角的正切值为
| 2 |
考点:直线与平面所成的角,点、线、面间的距离计算
专题:综合题,空间位置关系与距离,空间角
分析:(1)取AB的中点E,连接DE,BD,SE,证明AB⊥平面SDE,即可证明AB⊥SD.
(2)在平面SDE中,过S作SH⊥DE于H,SH的长即为S到平面ABCD的距离;
(3)F为AS的中点,利用向量法求解即可;
(4)P为AB的中点,利用向量法求解即可
(2)在平面SDE中,过S作SH⊥DE于H,SH的长即为S到平面ABCD的距离;
(3)F为AS的中点,利用向量法求解即可;
(4)P为AB的中点,利用向量法求解即可
解答:
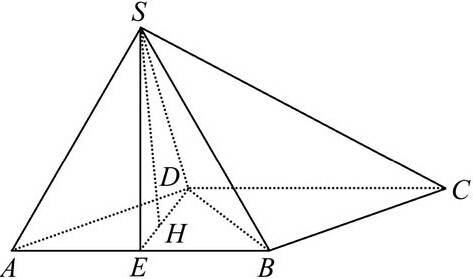 (1)证明:如图,取AB的中点E,连接DE,BD,SE,
(1)证明:如图,取AB的中点E,连接DE,BD,SE,
∵底面ABCD是菱形,∠BAD=60°,
∴BD=2,△ABD为正三角形.
又∵E为AB的中点,∴DE⊥AB.
又∵SA=SB,∴SE⊥AB.
又∵SE∩DE=E,
∴AB⊥平面SDE.
∵SD?平面SDE,∴AB⊥SD.
(2)解:在平面SDE中,过S作SH⊥DE于H.
∵AB⊥平面SDE,∴AB⊥SH.
又∵AB∩DE=E,∴SH⊥平面ABD.
∴SH的长即为S到平面ABCD的距离.
在△ABD中,AB=AD=BD=2,∴DE=
,
在△SAB中,SA=SB=AB=2,∴SE=
.
在等腰△SDE中,SD=2,
(3)解:假设AS上存在点F使GF∥平面SBC,连接BD,以正三角形ABD的中心O为原点,OA为x轴,OS为z轴,平行于BD的且过点O的直线为y轴,建立如图所示的空间直角坐标系.
A(
,0,0),B(-
,1,0),C(-
,0,0),
D(-
,-1,0),S(0,0,
),G(-
,-
,0),
=(-
,0,
),
设
=λ
=λ(-
,0,
),
∴F(-
λ+
,0,
λ),
=(-
λ+
,
,
λ),
=(-
,-1,0),
=(-
,0,-
).
设平面SBC的一个法向量为
=(x,y,z),则有
-
x-y=0,-
x-
z=0.
令x=1,则y=-
,z=-
,
即
=(1,-
,-
).
则有
•
=0,
即(-
λ+
)+(-
)+
λ×(-
)=0.
化简得-2
λ+
=0,解得λ=
.
故
=
,即F为AS的中点.
(4)解:假设线段AB上存在这样的点P使SP与平面SCD所成的角的正切值为
,
即所成角的正弦值为
,
=(-
,1,0),设
=λ1
=(-
λ1,λ1,0),
则P(-
λ1+
,λ1,0),
=(-
λ1+
,λ1,-
),
=(-
,0,-
),
=(
,-1,0).
设平面SDC的一个法向量为n1=(x1,y1,z1),
则n1•
=0,n1•
=0,
解得n1=(1,
,-
).
cos<
,n1>=
=
,代入,解得λ1=
.
故P为AB的中点.
 (1)证明:如图,取AB的中点E,连接DE,BD,SE,
(1)证明:如图,取AB的中点E,连接DE,BD,SE,∵底面ABCD是菱形,∠BAD=60°,
∴BD=2,△ABD为正三角形.
又∵E为AB的中点,∴DE⊥AB.
又∵SA=SB,∴SE⊥AB.
又∵SE∩DE=E,
∴AB⊥平面SDE.
∵SD?平面SDE,∴AB⊥SD.
(2)解:在平面SDE中,过S作SH⊥DE于H.
∵AB⊥平面SDE,∴AB⊥SH.
又∵AB∩DE=E,∴SH⊥平面ABD.
∴SH的长即为S到平面ABCD的距离.
在△ABD中,AB=AD=BD=2,∴DE=
| 3 |
在△SAB中,SA=SB=AB=2,∴SE=
| 3 |
在等腰△SDE中,SD=2,
|
(3)解:假设AS上存在点F使GF∥平面SBC,连接BD,以正三角形ABD的中心O为原点,OA为x轴,OS为z轴,平行于BD的且过点O的直线为y轴,建立如图所示的空间直角坐标系.

A(
| 2 |
| 3 |
| 3 |
| ||
| 3 |
| 4 |
| 3 |
| 3 |
D(-
| ||
| 3 |
| 2 |
| 3 |
| 6 |
| 5 |
| 6 |
| 3 |
| 1 |
| 2 |
| AS |
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
| 6 |
设
| AF |
| AS |
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
| 6 |
∴F(-
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
| 6 |
| GF |
| 2 |
| 3 |
| 3 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 6 |
| BC |
| 3 |
| SC |
| 4 |
| 3 |
| 3 |
| 2 |
| 3 |
| 6 |
设平面SBC的一个法向量为
| n |
-
| 3 |
| 4 |
| 3 |
| 3 |
| 2 |
| 3 |
| 6 |
令x=1,则y=-
| 3 |
| 2 |
即
| n |
| 3 |
| 2 |
则有
| GF |
| n |
即(-
2
| ||
| 3 |
3
| ||
| 2 |
| ||
| 2 |
| 2 |
| 3 |
| 6 |
| 2 |
化简得-2
| 3 |
| 3 |
| 1 |
| 2 |
故
| AF |
| 1 |
| 2 |
| AS |
(4)解:假设线段AB上存在这样的点P使SP与平面SCD所成的角的正切值为
| 2 |
即所成角的正弦值为
| ||
| 3 |
| AB |
| 3 |
| AP |
| AB |
| 3 |
则P(-
| 3 |
| 2 |
| 3 |
| 3 |
| SP |
| 3 |
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
| 6 |
| SC |
| 4 |
| 3 |
| 3 |
| 2 |
| 3 |
| 6 |
| CD |
| 3 |
设平面SDC的一个法向量为n1=(x1,y1,z1),
则n1•
| SC |
| CD |
解得n1=(1,
| 3 |
| 2 |
cos<
| SP |
|
| ||
|
|
| ||
| 3 |
| 1 |
| 2 |
故P为AB的中点.
点评:本题考查直线与平面所成的角,考查点、线、面间的距离计算,考查向量法,考查学生分析解决问题的能力,考查学生的计算能力,有难度.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
