题目内容
 微积分的创立与求曲线的切线是密不可分的,历史上有很多关于曲线的研究.如图,设PN是曲线的切线,下面是两位数学家的说法:
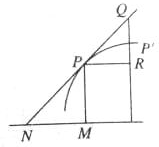
微积分的创立与求曲线的切线是密不可分的,历史上有很多关于曲线的研究.如图,设PN是曲线的切线,下面是两位数学家的说法:①数学家Barrow认为:当弧PP′足够小(PP′→0)时,有
| PM |
| NM |
| P′R |
| PR |
②数学家Leibniz认为:令PR=dx,P′R=dy,当dx→0时,有PM→
| dy |
| dx |
则( )
| A、Barrow正确,Leibniz错误 |
| B、Leibniz正确,Barrow错误 |
| C、Barrow,Leibniz都正确 |
| D、Barrow,Leibniz都错误 |
考点:微积分的产生──划时代的成就,微积分基本定理
专题:极限思想
分析:微积分的思想为极限的思想,即可得到答案.
解答:
解:当弧PP′足够小时,三角形PMN与三角形P′RP可看成是相似的,
故数学家Barrow说法正确.同理可得Leibniz说法正确.
故:选C.
故数学家Barrow说法正确.同理可得Leibniz说法正确.
故:选C.
点评:本题考查微积分的极限思想,属基础题.

练习册系列答案
相关题目
已知f(1)=1,f(x)=
(x=2,3,…),m∈N+,则f(2m)=( )
|
| A、2m+1 | |||||
B、
| |||||
C、
| |||||
| D、3m2+2m |
在正四棱锥P-ABCD中,PA=
AB,M是BC的中点,G是△PAD的重心,则在平面PAD中经过点G且与直线PM垂直的直线条数有( )
| ||
| 2 |
| A、0条 | B、1条 | C、3条 | D、无数条 |
数列an=
的前5项之和是( )
| 1+(-1)n |
| 2 |
| A、0 | B、2 | C、4 | D、6 |
 在空间四边形ABCD中,E、F、G、H分别是边AB、BC、CD、DA的中点,对角线AC=BD=2,且AC⊥BD,则四边形EFGH的面积为
在空间四边形ABCD中,E、F、G、H分别是边AB、BC、CD、DA的中点,对角线AC=BD=2,且AC⊥BD,则四边形EFGH的面积为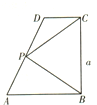 如图所示,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2,CD=1,BC=a(a>0),P为线段AD(含端点)上一个动点,设
如图所示,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2,CD=1,BC=a(a>0),P为线段AD(含端点)上一个动点,设