题目内容
在正四棱锥P-ABCD中，PA=
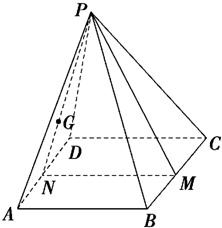
AB，M是BC的中点，G是△PAD的重心，则在平面PAD中经过点G且与直线PM垂直的直线条数有（ ）
| ||
| 2 |
| A、0条 | B、1条 | C、3条 | D、无数条 |
考点：直线与平面垂直的判定
专题：综合题,探究型,空间位置关系与距离
分析：根据正四棱锥P-ABCD中，PA=
AB，M是BC的中点，利用勾股定理即可求出PM与AB的关系，利用勾股定理证明PM⊥PN，利用线面垂直的判定定理可证PM⊥面PAD，因此可求平面PAD中经过G点且与直线PM垂直的直线的条数．
| ||
| 2 |
解答：
解：设正四棱锥的底面边长为a，则侧棱长为
a．
由PM⊥BC，可得PM=
a．
连接PG并延长与AD相交于N点，则求得PN=
a，MN=AB=a，
∴PM2+PN2=MN2，
∴PM⊥PN，又PM⊥AD，
∴PM⊥面PAD，
∴在平面PAD中经过G点的任意一条直线都与PM垂直．
故答案为无数．
解：设正四棱锥的底面边长为a，则侧棱长为
| ||
| 2 |
由PM⊥BC，可得PM=
| ||
| 2 |
连接PG并延长与AD相交于N点，则求得PN=
| ||
| 2 |
∴PM2+PN2=MN2，
∴PM⊥PN，又PM⊥AD，
∴PM⊥面PAD，
∴在平面PAD中经过G点的任意一条直线都与PM垂直．
故答案为无数．
点评：本题主要考查了直线与平面垂直的判断和性质定理，以及空间中直线的位置关系，考查了学生利用知识分析解决问题的能力，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
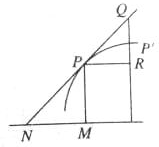微积分的创立与求曲线的切线是密不可分的，历史上有很多关于曲线的研究．如图，设PN是曲线的切线，下面是两位数学家的说法：①数学家Barrow认为：当弧PP′足够小（PP′→0）时，有
| PM |
| NM |
| P′R |
| PR |
②数学家Leibniz认为：令PR=dx，P′R=dy，当dx→0时，有PM→
| dy |
| dx |
则（ ）
| A、Barrow正确，Leibniz错误 |
| B、Leibniz正确，Barrow错误 |
| C、Barrow，Leibniz都正确 |
| D、Barrow，Leibniz都错误 |
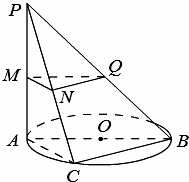如图，⊙O在平面α内，AB是⊙O的直径，PA⊥平面α，C为圆周上不同于A、B的任意一点，M，N，Q分别是PA，PC，PB的中点．