题目内容
(2009•海南•宁夏高考)已知
=(-3,2),
=(-1,0),向量λ
+
与
-2
垂直,则实数λ的值为( )
| a |
| b |
| a |
| b |
| a |
| b |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
考点:数量积判断两个平面向量的垂直关系
专题:平面向量及应用
分析:由向量的数乘运算及坐标加减法运算求得向量λ
+
与
-2
的坐标,然后直接利用向量垂直的坐标表示求解.
| a |
| b |
| a |
| b |
解答:
解:由
=(-3,2),
=(-1,0),得
λ
+
=λ(-3,2)+(-1,0)=(-3λ-1,2λ),
-2
=(-3,2)-2(-1,0)=(-1,2).
∵λ
+
与
-2
垂直,
∴(-1)×(-3λ-1)+2×2λ=0,
解得:λ=-
.
故选:A.
| a |
| b |
λ
| a |
| b |
| a |
| b |
∵λ
| a |
| b |
| a |
| b |
∴(-1)×(-3λ-1)+2×2λ=0,
解得:λ=-
| 1 |
| 7 |
故选:A.
点评:本题考查向量的数量积判断两个向量的垂直关系,考查计算能力,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
f(x)=ax3-2x2-3,若f′(1)=5,则a等于( )
| A、5 | B、4 | C、2 | D、3 |
-60°角是第( )象限角.
| A、一 | B、二 | C、三 | D、四 |
已知数列{an},{bn}(n∈N*)都是公差为1的等差数列,其首项分别为a1,b1,且a1+b1=5,则数列{an+bn}的前10项的和等于( )
| A、85 | B、95 |
| C、120 | D、140 |
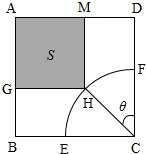 如图,体育馆计划用运动场的边角地建造一个矩形健身室,四边形ABCD是一块正方形地皮,边长为a(a>40m),扇形CEF是运动场的一部分,半径为40m,矩形AGHM就是计划的健身室,其中G、M分别在AB、AD上,H在
如图,体育馆计划用运动场的边角地建造一个矩形健身室,四边形ABCD是一块正方形地皮,边长为a(a>40m),扇形CEF是运动场的一部分,半径为40m,矩形AGHM就是计划的健身室,其中G、M分别在AB、AD上,H在