题目内容
10.(4x-2-x)8展开式中含2x项的系数是( )| A. | -56 | B. | -28 | C. | 28 | D. | 56 |
分析 根据(4x-2-x)8展开式的通项公式,即可求出展开式中含2x项的系数.
解答 解:(4x-2-x)8展开式的通项公式为:
Tr+1=${C}_{8}^{r}$•4x(8-r)•(-1)r•2-xr=(-1)r•${C}_{8}^{r}$•2x(16-3r),
令16-3r=1,解得r=5;
所以,展开式中含2x项的系数为
(-1)5•${C}_{8}^{5}$•=-56.
故选:A.
点评 本题考查了利用二项式展开式的通项公式求特定项的应用问题,是基础题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.已知不等式组$\left\{\begin{array}{l}x+y≤1\\ x-y≥-1\\ y≥0\end{array}\right.$所表示的平面区域为D,若直线(m+2)x-(m+1)y+2=0与平面区域D有公共点,则实数m的取值范围为( )
| A. | (-4,0) | B. | [-4,0] | C. | (-∞,-4)∪(0,+∞) | D. | (-∞,-4]∪[0,+∞) |
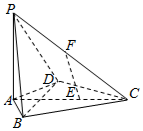 在四棱锥P-ABCD中,PA⊥底面ABCD,AB=AD=2,CB=CD=$\sqrt{7}$,∠BAD=120°,点E在线段AC上,且AE=2EC,F为线段PC的中点.
在四棱锥P-ABCD中,PA⊥底面ABCD,AB=AD=2,CB=CD=$\sqrt{7}$,∠BAD=120°,点E在线段AC上,且AE=2EC,F为线段PC的中点. 如图,三棱锥S-ABC,E、F分别在线段AB、AC上,EF∥BC,△ABC、△SEF均是等边三角形,且平面SEF⊥平面ABC,若BC=4,EF=a,O为EF的中点.
如图,三棱锥S-ABC,E、F分别在线段AB、AC上,EF∥BC,△ABC、△SEF均是等边三角形,且平面SEF⊥平面ABC,若BC=4,EF=a,O为EF的中点.