题目内容
1.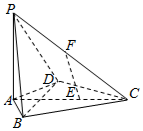 在四棱锥P-ABCD中,PA⊥底面ABCD,AB=AD=2,CB=CD=$\sqrt{7}$,∠BAD=120°,点E在线段AC上,且AE=2EC,F为线段PC的中点.
在四棱锥P-ABCD中,PA⊥底面ABCD,AB=AD=2,CB=CD=$\sqrt{7}$,∠BAD=120°,点E在线段AC上,且AE=2EC,F为线段PC的中点.(1)求证:EF∥平面PBD
(2)若PC=5,三棱锥F-PAD的体积.
分析 (1)设AC∩BD=O,连接PO,通过证明EF为△POC的中位线,推出EF∥PO,然后EF∥平面PBD.
(2)利用VF-PAD=$\frac{1}{2}$VC-PAD=$\frac{1}{2}$VP-CAD,求解几何体的体积即可.
解答 (本小题满分12分)
(1)证明:∵AB=AD,CB=CD,∴AC⊥BD,设AC∩BD=O,连接PO,由AB=AD=2,∠BAD=120°
得:OA=1,BD=2$\sqrt{3}$,在Rt△COD中,CD=$\sqrt{7}$,OD=$\sqrt{3}$∴OC=2
∵AE=2EC∴E为OC中点 又∵F为PC的中点∴EF为△POC的中位线
∴EF∥PO 又PO?面PBD EF?面PBD
∴EF∥平面PBD…(6分)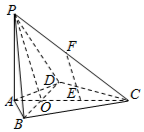
(2)解:在Rt△PAC中,PC=5,AC=3∴PA=4
∴VF-PAD=$\frac{1}{2}$VC-PAD=$\frac{1}{2}$VP-CAD=$\frac{1}{2}$×$\frac{1}{2}$VP-ABCD=$\frac{1}{4}$×$\frac{1}{3}$×$\frac{1}{2}$×3×2$\sqrt{3}$×4=$\sqrt{3}$…(12分)
点评 本题考查直线与平面平行的证明,几何体的体积的求法,考查转化思想以及计算能力.

练习册系列答案
相关题目
6.某同学有6本工具书,其中语文1本、英语2本、数学3本,现在他把这6本书放到书架上排成一排,则同学科工具书都排在一起的概率是( )
| A. | $\frac{1}{30}$ | B. | $\frac{1}{15}$ | C. | $\frac{1}{10}$ | D. | $\frac{1}{5}$ |
10.(4x-2-x)8展开式中含2x项的系数是( )
| A. | -56 | B. | -28 | C. | 28 | D. | 56 |
11.已知集合A={x|x2<1},B={x|2x<1},则A∩B=( )
| A. | (-1,0) | B. | (-1,1) | C. | (-∞,0] | D. | (-∞,1) |