题目内容
18.若实数x,y满足$\left\{\begin{array}{l}{x≥k}\\{x-2y+4≥0}\\{2x-y-4≤0}\\{\;}\end{array}\right.$,若z=2x+y的最小值为8,则k=3.分析 画出满足条件的平面区域,求出角点的坐标,结合函数的图象,解出k的值即可.
解答  解:画出满足条件的平面区域,如图示
解:画出满足条件的平面区域,如图示
由$\left\{\begin{array}{l}{x=k}\\{2x-y-4=0}\end{array}\right.$,解得A(k,2k-4),
由图象得直线z=2x+y过A时,z最小是8,
∴8=2k+2k-4,解得:k=3,
故答案为:3.
点评 本题考查了简单的线性规划问题,考查数形结合思想,是一道中档题.

练习册系列答案
相关题目
6.某同学有6本工具书,其中语文1本、英语2本、数学3本,现在他把这6本书放到书架上排成一排,则同学科工具书都排在一起的概率是( )
| A. | $\frac{1}{30}$ | B. | $\frac{1}{15}$ | C. | $\frac{1}{10}$ | D. | $\frac{1}{5}$ |
3.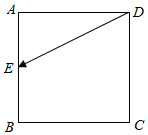 如图所示,已知正方形ABCD的边长为1,点E从D点出发,按字母顺序D→A→B→C沿线段DA,AB,BC运动到C点,在此过程中$\overrightarrow{DE}•\overrightarrow{CD}$的最大值是( )
如图所示,已知正方形ABCD的边长为1,点E从D点出发,按字母顺序D→A→B→C沿线段DA,AB,BC运动到C点,在此过程中$\overrightarrow{DE}•\overrightarrow{CD}$的最大值是( )
 如图所示,已知正方形ABCD的边长为1,点E从D点出发,按字母顺序D→A→B→C沿线段DA,AB,BC运动到C点,在此过程中$\overrightarrow{DE}•\overrightarrow{CD}$的最大值是( )
如图所示,已知正方形ABCD的边长为1,点E从D点出发,按字母顺序D→A→B→C沿线段DA,AB,BC运动到C点,在此过程中$\overrightarrow{DE}•\overrightarrow{CD}$的最大值是( )| A. | 0 | B. | $\frac{1}{2}$ | C. | 1 | D. | -1 |
10.(4x-2-x)8展开式中含2x项的系数是( )
| A. | -56 | B. | -28 | C. | 28 | D. | 56 |
7.不在3x+2y>3表示的平面区域内的点是( )
| A. | (0,0) | B. | (1,1) | C. | (0,2) | D. | (2,0) |
8.曲线f(x)=x3-x+3在点P处的切线平行于直线y=2x-1,则P点的坐标为( )
| A. | (1,3) | B. | (-1,3) | C. | (1,3)和(-1,3) | D. | (1,-3) |