题目内容
5.设$a=\frac{1}{2}sin{2°}+\frac{{\sqrt{3}}}{2}cos{2°}$,b=1-2sin213°,$c=\frac{{\sqrt{3}}}{2}$,则a,b,c的大小关系是c<a<b.(从小到大排列)分析 根据两角和的正弦公式求出a=sin62°,根据倍角公式求出b=64°,根据三角函数值求出c=60°,从而判断出a,b,c的大小即可.
解答 解:∵$a=\frac{1}{2}sin{2°}+\frac{{\sqrt{3}}}{2}cos{2°}$=sin62°,
b=1-2sin213°=cos26°=sin64°,
$c=\frac{{\sqrt{3}}}{2}$=sin60°,
则c<a<b,
故答案为:c<a<b.
点评 本题考查了三角函数的化简求值问题,熟练掌握三角函数的恒等变化公式是解题的关键,本题是一道基础题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目
10.(4x-2-x)8展开式中含2x项的系数是( )
| A. | -56 | B. | -28 | C. | 28 | D. | 56 |
14.汽车4S店是一种以“四位一体”为核心的特许经营模式,包括整车销售、零配件销售、售后服务、信息反馈等.某品汽车4S店为了了解A、B、C三种类型汽车质量问题,对售出的三种类型汽车各取100辆进行跟踪服务,发现各车型一年内需要维修的车辆如下表所示1:
表1
(1)某公司一次性从4S店购买该品牌A、B、C型汽车各一辆,记ξ表示这三辆车的一年内需要维修的车辆数,求ξ的分布列及数学期望(各型汽车维修的频率视为其需要维修的概率);
(2)该品牌汽车4S店为了对厂家新研发的一种产品进行合理定价,将该产品按使事先拟定的各种价格进行试销相等时间,得到数据如表2.
表2
预计在今后的销售中,销量与单价仍然服从$\widehat{y}$=bx+a(b=0.2,a=$\widehat{y}$-b$\widehat{x}$)的关系,且该产品的成本是500元/件,为使4S店获得最大利润(利润=销售收入-成本),该产品的单价应定位多少元.
| 车型 | A型 | B型 | C型 |
| 频数 | 20 | 20 | 40 |
(1)某公司一次性从4S店购买该品牌A、B、C型汽车各一辆,记ξ表示这三辆车的一年内需要维修的车辆数,求ξ的分布列及数学期望(各型汽车维修的频率视为其需要维修的概率);
(2)该品牌汽车4S店为了对厂家新研发的一种产品进行合理定价,将该产品按使事先拟定的各种价格进行试销相等时间,得到数据如表2.
| 单价x(元) | 800 | 820 | 840 | 850 | 880 | 900 |
| 销量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
预计在今后的销售中,销量与单价仍然服从$\widehat{y}$=bx+a(b=0.2,a=$\widehat{y}$-b$\widehat{x}$)的关系,且该产品的成本是500元/件,为使4S店获得最大利润(利润=销售收入-成本),该产品的单价应定位多少元.
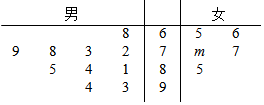 某校组织学生参加数学竞赛,共有15名学生获奖,其中10名男生和5名女生,其成绩如茎叶图所示(单位:分).规定:成绩在80分以上者为一等奖,80分以下者为二等奖,已知这5名女生的平均成绩为73.
某校组织学生参加数学竞赛,共有15名学生获奖,其中10名男生和5名女生,其成绩如茎叶图所示(单位:分).规定:成绩在80分以上者为一等奖,80分以下者为二等奖,已知这5名女生的平均成绩为73.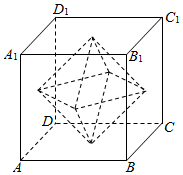 如图所示,用一棱长为a的正方体,制作一以各面中心为顶点的正八面体.求:
如图所示,用一棱长为a的正方体,制作一以各面中心为顶点的正八面体.求: