题目内容
15.已知△ABC中,角A、$\frac{3}{2}{B}$、C成等差数列,且△ABC的面积为$1+\sqrt{2}$,则AC边的最小值是2.分析 由已知及等差数列的性质可得A+C=3B,结合三角形内角和定理可求B的值,利用三角形面积公式可得$ac=2(2+\sqrt{2})$,利用余弦定理及基本不等式即可解得AC边的最小值.
解答 解:∵A、$\frac{3}{2}$B、C成等差数列,
∴A+C=3B,
又∵A+B+C=π,
∴$B=\frac{π}{4}$,
∴由${S_{△ABC}}=\frac{1}{2}acsinB=1+\sqrt{2}$得$ac=2(2+\sqrt{2})$,
∵b2=a2+c2-2accosB=${a^2}+{c^2}-\sqrt{2}ac$,及a2+c2≥2ac,
∴${b^2}≥(2-\sqrt{2})ac=4$,解得:b≥2,
∴b的最小值为2.
故答案为:2.
点评 本题主要考查了等差数列的性质,三角形内角和定理,三角形面积公式,余弦定理,基本不等式在解三角形中的应用,考查了计算能力和转化思想,属于中档题.

练习册系列答案
相关题目
7.2015年9月3日,抗日战争胜利70周年纪念活动在北京隆重举行,受到世界人民的瞩目.纪念活动包括举行纪念大会、阅兵式、招待会等环节.受邀抗战老兵由于身体原因,可选择参加纪念大会、阅兵式、招待会中某几个环节,也可都不参加.现从受邀抗战老兵中随机选取60人进行统计分析,得到参加纪念活动的环节数及其概率如表所示:
(Ⅰ)若a=2b,按照参加纪念活动的环节数,从这60名抗战老兵中分层选取6人进行座谈,求参加纪念活动环节数为2的抗战老兵中选取的人数;
(Ⅱ)某医疗部门决定从(Ⅰ)中选取的6名抗战老兵中随机选取2名进行体检,求这2名抗战老兵中至少有1人参加纪念活动的环节数为3的概率.
| 参加纪念活动的环节数 | 0 | 1 | 2 | 3 |
| 概率 | $\frac{1}{6}$ | a | b | $\frac{1}{3}$ |
(Ⅱ)某医疗部门决定从(Ⅰ)中选取的6名抗战老兵中随机选取2名进行体检,求这2名抗战老兵中至少有1人参加纪念活动的环节数为3的概率.
6.某同学有6本工具书,其中语文1本、英语2本、数学3本,现在他把这6本书放到书架上排成一排,则同学科工具书都排在一起的概率是( )
| A. | $\frac{1}{30}$ | B. | $\frac{1}{15}$ | C. | $\frac{1}{10}$ | D. | $\frac{1}{5}$ |
3.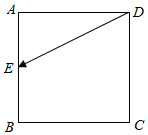 如图所示,已知正方形ABCD的边长为1,点E从D点出发,按字母顺序D→A→B→C沿线段DA,AB,BC运动到C点,在此过程中$\overrightarrow{DE}•\overrightarrow{CD}$的最大值是( )
如图所示,已知正方形ABCD的边长为1,点E从D点出发,按字母顺序D→A→B→C沿线段DA,AB,BC运动到C点,在此过程中$\overrightarrow{DE}•\overrightarrow{CD}$的最大值是( )
 如图所示,已知正方形ABCD的边长为1,点E从D点出发,按字母顺序D→A→B→C沿线段DA,AB,BC运动到C点,在此过程中$\overrightarrow{DE}•\overrightarrow{CD}$的最大值是( )
如图所示,已知正方形ABCD的边长为1,点E从D点出发,按字母顺序D→A→B→C沿线段DA,AB,BC运动到C点,在此过程中$\overrightarrow{DE}•\overrightarrow{CD}$的最大值是( )| A. | 0 | B. | $\frac{1}{2}$ | C. | 1 | D. | -1 |
10.(4x-2-x)8展开式中含2x项的系数是( )
| A. | -56 | B. | -28 | C. | 28 | D. | 56 |
20.设变量x,y满足约束条件$\left\{\begin{array}{l}{2x-y-2≤0}\\{x-2y+2≥0}\\{x+y-1≥0}\end{array}\right.$,则M=$\frac{y-x}{x+2}$的取值范围是( )
| A. | [-$\frac{1}{3}$,$\frac{1}{2}$] | B. | [-$\frac{1}{2}$,1] | C. | [$\frac{1}{2}$,2] | D. | [$\frac{2}{3}$,$\frac{3}{2}$] |
7.不在3x+2y>3表示的平面区域内的点是( )
| A. | (0,0) | B. | (1,1) | C. | (0,2) | D. | (2,0) |
3.A,B是平面α外不同的两个定点,P为平面α内动点,且cos∠PAB=$\frac{1}{3}$,则P点的轨迹是( )
| A. | 圆或椭圆 | B. | 抛物线或双曲线 | C. | 椭圆或双曲线 | D. | 以上都有可能 |