题目内容
7.奇函数f(x)的定义域为R,若f(x+2)为偶函数,且f(1)=1,则f(100)+f(101)=-1.分析 根据函数奇偶性的性质求出函数的周期,利用周期性和奇偶性进行转化即可.
解答 解:偶函数f(x)的定义域为R,若f(x+2)为奇函数,
∴f(-x+2)=-f(x+2)=f(x-2),
即-f(x+4)=f(x),
则f(x+4)=-f(x),f(x+8)=-f(x+4)=f(x),
即函数的周期是8的周期函数,
则f(100)=f(4)=-f(0)=0,
f(101)=f(5)=-f(1)=-1,
∴f(100)+f(101)=-1,
故答案为:-1.
点评 本题考查的知识点是函数奇偶性的性质,熟练掌握函数奇偶性的性质,是解答的关键.

练习册系列答案
相关题目
2.设向量$\overrightarrow{a}$=(1,2),|$\overrightarrow{b}$|=2$\sqrt{5}$,$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为60°则$\overrightarrow{a}$•$\overrightarrow{b}$的值为( )
| A. | $\sqrt{5}$ | B. | 5 | C. | 5$\sqrt{5}$ | D. | 10 |
12.正项等比数列{an}中,a1a3+2a2a3+a1a5=16,则a2+a3的值为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
19.考取驾照是一个非常严格的过程,有的人并不能一次性通过,需要进行补考,现在有一张某驾校学员第一次考试结果汇总表:
(1)完成列联表
(2)根据列联表判断性别与考试成绩是否有关系,如果有关系求出精确地可信度,没关系请说明理由.
| 成绩 性别 | 合格 | 不合格 | 合计 |
| 男性 | 45 | 10 | |
| 女性 | 30 | ||
| 合计 | 105 |
(2)根据列联表判断性别与考试成绩是否有关系,如果有关系求出精确地可信度,没关系请说明理由.
16.已知直角△ABC中,∠C=90°,∠B=30°,AB=4,D为AB的中点,沿中线将△ACD折起使得AB=$\sqrt{13}$,则二面角A-CD-B的大小为( )
| A. | 60° | B. | 90° | C. | 120° | D. | 150° |
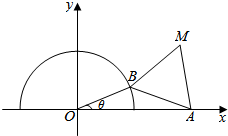 如图,已知半圆O:x2+y2=1(y≥0)及点A(2,0),B为半圆周上任意一点,以AB为一边作等边△ABM.设∠AOB=θ,其中0<θ<π.
如图,已知半圆O:x2+y2=1(y≥0)及点A(2,0),B为半圆周上任意一点,以AB为一边作等边△ABM.设∠AOB=θ,其中0<θ<π.