题目内容

若x∈（0，
π
2
），则不等式
sin2(x+
π
4
)+a
sin2x
+sin2x≥5恒成立的正实数a的取值范围为
 
．
考点：三角函数的最值
专题：三角函数的求值
分析：由题意可得sin2x＞0，
1
sin2x
+
a
sin2x
+sin2x≥
9
2
 恒成立．利用基本不等式可得
1
sin2x
+
2a
sin2x
+sin2x≥2
2a
，可得 2
2a
≥
9
2
，由此求得a的范围．
解答： 解：由题意可得sin2x＞0，且
1+sin2x+2a
2sin2x
+sin2x≥5恒成立，即
1
sin2x
+
a
sin2x
+sin2x≥
9
2
 恒成立．
利用基本不等式可得 即
1
sin2x
+
2a
sin2x
+
1
2
sin2x+
1
2
sin2x≥4
a
2
=2
2a
，当且仅当
1
sin2x
=
2a
sin2x
=
1
2
sin2x 时取等号．
∴2
2a
≥
9
2
，求得a≥
81
32
，
故答案为：[
81
32
，+∞）．
点评：本题主要考查半角公式、基本不等式的应用，函数的恒成立问题，属于基础题．
练习册系列答案
相关题目
已知函数f（x）=
1+lnx
x
．
（Ⅰ）若函数f（x）在区间（m，m+
1
3
）（m＞0）上存在极值，求实数m的取值范围；
（Ⅱ）设g（x）=
1+x
a(1-x)
[xf（x）-1]，若对任意x∈（0，1）恒有g（x）＜-2，求实数a的取值范围．
函数f（x）=
1
2
sin（ωx-
π
3
）（ω＞0）的图象在[
π
4
，
π
2
]上为增函数，则ω的取值范围为（　　）
A、[
2
3
，
5
3
]
B、[
17
3
，
22
3
]
C、(0，
5
3
]
D、(0，
17
3
]
已知数列{an}中，a1=1，a2=4，满足an+2=
5
3
an+1-
2
3
an，则数列{an}的通项公式an=
 
．
已知△ABC的角A，B，C所对应的边分别为a，b，c，且cosB=
4
5
，a=10，S△ABC=42，则b+
a
sinA
=（　　）
A、
27
2
2
B、16
C、8
2
D、16
2
已知曲线ax2+by2=12的两条动弦MA，MB所在直线的斜率分别为k1，k2．
（1）已知a=b=3且A（-2，0），B（2，0），试证明：k1k2为定值．
（2）已知a=3，b=4．
（i）若A（-2，0），B（2，0），试判断k1k2是否为定值？若是，求出定值；若不是，请说明理由．
（ii）若定点M（1，-
3
2
）且k1k2=
3
4
，试判断直线AB是否过一定点？若是，求出定点坐标；若不是，请说明理由．
在二项式(2
x
+
1
4x
)n的展开式中，前三项的系数成等差数列，则该二项式展开式中x-2项的系数为（　　）
A、1B、4C、8D、16
已知某几何体的三视图如图所示（单位cm），则此几何体的体积为（　　）
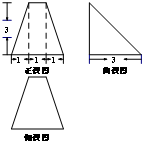
A、
21
2
cm3
B、
15
2
cm3
C、16cm3
D、12cm3
运行如图所示的流程图，则输出的结果an是（　　）
A、1B、-1C、-4D、-5

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网