题目内容
已知函数f(x)=
.
(Ⅰ)若函数f(x)在区间(m,m+
)(m>0)上存在极值,求实数m的取值范围;
(Ⅱ)设g(x)=
[xf(x)-1],若对任意x∈(0,1)恒有g(x)<-2,求实数a的取值范围.
| 1+lnx |
| x |
(Ⅰ)若函数f(x)在区间(m,m+
| 1 |
| 3 |
(Ⅱ)设g(x)=
| 1+x |
| a(1-x) |
考点:利用导数求闭区间上函数的最值,利用导数研究函数的极值
专题:导数的综合应用
分析:(Ⅰ)求出函数的极值,在探讨函数在区间 (m,m+
)(其中a>0)上存在极值,寻找关于m的不等式,求出实数m的取值范围;
(Ⅱ)先求导,再构造函数h(x)=lnx+
,求出h(x)的最大值小于0即可.
| 1 |
| 3 |
(Ⅱ)先求导,再构造函数h(x)=lnx+
| 2a(1-x) |
| 1+x |
解答:
解:(Ⅰ)因为函数f(x)=
,
所以f′(x)=-
(x>0).极值点为f′(x)=0解得x=1,
当0<x<1时,f'(x)>0;
当x>1时,f'(x)<0.
所以f(x)在(0,1)上单调递增;在(1,+∞)上单调递减,所以函数f(x)在x=1处取得极大值.
故m<1<m+
,解得
<m<1.
即实数m的取值范围为(
,1).
(Ⅱ)由题意知,a≠0,且g(x)=
lnx,因为x∈(0,1),所以
lnx<0,
当a<0时,g(x)>0,不合题意,
当a>0时,由g(x)<-2,可得lnx+
<0恒成立,
设h(x)=lnx+
,则hmax(x)<0,
∴h′(x)=
设t(x)=x2+(2-4a)x+1,△=(2-4a)2-4=16a(a-1).
(1)当0<a≤1时,△≤0,此时:t(x)≥0,h'(x)≥0,所以h(x)在(0,1)内单调递增,又h(1)=0,
所以h(x)<h(1)=0.所以0<a≤1符合条件
(2)当a>1时,△>0,注意到t(0)=1>0,t(1)=4(1-a)<0,所以存在x0∈(0,1),使得t(x0)=0,于是对任意x∈(x0,1),t(x)<0,h'(x)<0.则h(x)在(x0,1)内单调递减,又h(1)=0,所以当x∈(x0,1)时,h(x)>0,不合要求,
综合(1)(2)可得0<a≤1
| 1+lnx |
| x |
所以f′(x)=-
| lnx |
| x2 |
当0<x<1时,f'(x)>0;
当x>1时,f'(x)<0.
所以f(x)在(0,1)上单调递增;在(1,+∞)上单调递减,所以函数f(x)在x=1处取得极大值.
故m<1<m+
| 1 |
| 3 |
| 2 |
| 3 |
即实数m的取值范围为(
| 2 |
| 3 |
(Ⅱ)由题意知,a≠0,且g(x)=
| 1+x |
| a(1-x) |
| 1+x |
| 1-x |
当a<0时,g(x)>0,不合题意,
当a>0时,由g(x)<-2,可得lnx+
| 2a(1-x) |
| 1+x |
设h(x)=lnx+
| 2a(1-x) |
| 1+x |
∴h′(x)=
| x2+(2-4a)x+1 |
| x(1+x)2 |
设t(x)=x2+(2-4a)x+1,△=(2-4a)2-4=16a(a-1).
(1)当0<a≤1时,△≤0,此时:t(x)≥0,h'(x)≥0,所以h(x)在(0,1)内单调递增,又h(1)=0,
所以h(x)<h(1)=0.所以0<a≤1符合条件
(2)当a>1时,△>0,注意到t(0)=1>0,t(1)=4(1-a)<0,所以存在x0∈(0,1),使得t(x0)=0,于是对任意x∈(x0,1),t(x)<0,h'(x)<0.则h(x)在(x0,1)内单调递减,又h(1)=0,所以当x∈(x0,1)时,h(x)>0,不合要求,
综合(1)(2)可得0<a≤1
点评:本题考查极值的应用,应用满足条件的实数的取值范围的求法.解题时要认真审题,仔细解答,注意构造法和分类讨论法的合理运用.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
已知F1,F2是双曲线
-
=1(a>0,b>0)的焦点,以线段F1F2为边作正三角形MF1F2,若边MF1的中点在双曲线上,则双曲线的离心率是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、4+2
| ||||
B、
| ||||
C、
| ||||
D、
|
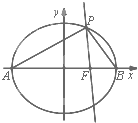 已知椭圆C的中心在坐标原点,右焦点为F(1,0),A,B是椭圆的左、右顶点,P是椭圆C上异于A,B的动点,且△APB面积的最大值为
已知椭圆C的中心在坐标原点,右焦点为F(1,0),A,B是椭圆的左、右顶点,P是椭圆C上异于A,B的动点,且△APB面积的最大值为
 如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,AB=1,BC=2,PA=2,E、F分别是AB、PC的中点.
如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,AB=1,BC=2,PA=2,E、F分别是AB、PC的中点.