题目内容
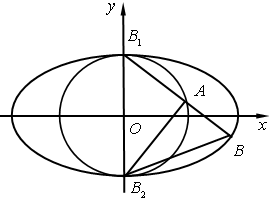
 如图,已知平面内一动点A到两个定点F1、F2的距离之和为4,线段F1F2的长为2
如图,已知平面内一动点A到两个定点F1、F2的距离之和为4,线段F1F2的长为2| 3 |
(1)求动点A的轨迹Γ的方程;
(2)过点F1作直线l与轨迹Γ交于A、C两点,且点A在线段F1F2的上方,线段AC的垂直平分线为m.
①求△AF1F2的面积的最大值;
②轨迹Γ上是否存在除A、C外的两点S、T关于直线m对称,请说明理由.
考点:直线与圆锥曲线的综合问题,轨迹方程
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)根据平面内一动点A到两个定点F1、F2的距离之和为4,线段F1F2的长为2
,可得轨迹是以F1、F2为焦点的椭圆,建立平面直角坐标系,可得动点A的轨迹Γ的方程;
(2)①当A在椭圆与y轴相交的地方,△AF1F2的高最大,面积最大,即可求△AF1F2的面积的最大值;
②当AC⊥F1F2时,存在除A、C外的两点S、T关于直线m对称,证明AC与F1F2不垂直时,不存在除A、C外的两点S、T关于直线m对称即可.
| 3 |
(2)①当A在椭圆与y轴相交的地方,△AF1F2的高最大,面积最大,即可求△AF1F2的面积的最大值;
②当AC⊥F1F2时,存在除A、C外的两点S、T关于直线m对称,证明AC与F1F2不垂直时,不存在除A、C外的两点S、T关于直线m对称即可.
解答:
解:(1)因为4>2
,所以轨迹是以F1、F2为焦点的椭圆,
以线段F1F2的中点为坐标原点,以F1F2所在直线为x轴建立平面直角坐标系,
可得动点A的轨迹Γ的方程为
+y2=1;
(2)①由题意,|F1F2|=2
,当A在椭圆与y轴相交的地方,△AF1F2的高最大,面积最大,
∴△AF1F2的面积的最大值为
•2
•1=
;
②当AC⊥F1F2时,存在除A、C外的两点S、T关于直线m对称,
下面证明AC与F1F2不垂直时,不存在除A、C外的两点S、T关于直线m对称.
假设存在这样的两个不同的点S(x3,y3),T(x4,y4),
设ST的中点为H(m,n),则kOH•kST=-
,kOMkAC=-
,
∴kOH=kOM=-
,
∴直线m过原点,斜率为-
≠-
∴假设不成立,
∴AC与F1F2不垂直时,不存在除A、C外的两点S、T关于直线m对称.
| 3 |
以线段F1F2的中点为坐标原点,以F1F2所在直线为x轴建立平面直角坐标系,
可得动点A的轨迹Γ的方程为
| x2 |
| 4 |
(2)①由题意,|F1F2|=2
| 3 |
∴△AF1F2的面积的最大值为
| 1 |
| 2 |
| 3 |
| 3 |
②当AC⊥F1F2时,存在除A、C外的两点S、T关于直线m对称,
下面证明AC与F1F2不垂直时,不存在除A、C外的两点S、T关于直线m对称.
假设存在这样的两个不同的点S(x3,y3),T(x4,y4),
设ST的中点为H(m,n),则kOH•kST=-
| 1 |
| 4 |
| 1 |
| 4 |
∴kOH=kOM=-
| 1 |
| 4k |
∴直线m过原点,斜率为-
| 1 |
| 4k |
| 1 |
| k |
∴假设不成立,
∴AC与F1F2不垂直时,不存在除A、C外的两点S、T关于直线m对称.
点评:本题考查椭圆的定义与方程,考查三角形面积的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
“a=±2”是“直线ax-4y+1=0与直线ax+y+1=0互相垂直”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
 已知椭圆C1:
已知椭圆C1: 定圆O的直径AB=2R,BC为⊙O的动弦,延长BC至D,使CD=BC,AC与OD交于P,求点P轨迹方程.
定圆O的直径AB=2R,BC为⊙O的动弦,延长BC至D,使CD=BC,AC与OD交于P,求点P轨迹方程. 如图,如果你在海边沿着海岸线直线前行,请设计一种测量海中两个小岛A,B之间距离的方法.
如图,如果你在海边沿着海岸线直线前行,请设计一种测量海中两个小岛A,B之间距离的方法.