题目内容

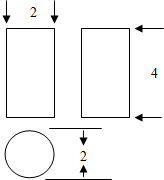
已知空间图形的三视图如图，空间几何体的表面积为（　　）
A、8πB、10π
C、12πD、9π
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：由已知中的三视图可得该几何体为一圆柱，求出圆柱的底面半径为高，代入圆柱表面积公式，可得答案．
解答： 解：由已知中的三视图可得该几何体为圆柱，
底面直径为1，即底面半径r=1，
高h=4，
故表面积S=2πr（r+h）=10π，
故选：B
点评：本题考查三视图复原几何体形状的判断，几何体的表面积与体积的求法，考查空间想象能力与计算能力．
练习册系列答案
相关题目
在等腰梯形ABCD中，E，F分别是底边AB，BC的中点，把四边形AEFD沿直线EF折起后所在的平面记为α，p∈α，设PB，PC与α所成的角分别为θ1，θ2（θ1，θ2均不为零）．若θ1=θ2，则满足条件的P所形成的图象是
 
．
设不等式组
6x-y≥8
2x-3y≤0
2x+y≤8
表示的平面区域为r，且函数y=logax的图象经过区域r，则实数a的取值范围是（　　）
A、（1，
3
]
B、[
42
，
3
2
]
C、[
42
，
3
]
D、[
3
2
，
3
]
若函数f（x）=loga（2x2+x）（a＞0，a≠1）在区间（
1
2
，1）内恒有f（x）＞0，则f（x）的单调递增区间是（　　）
A、（-∞，-
1
4
）
B、（-
1
4
，+∞）
C、（-∞，-
1
2
）
D、（0，+∞）
已知-1和2是函数y=x2+bx+c的两个零点，则不等式bx2+bx-c＜0的解集为（　　）
A、（-1，2）
B、（-2，1）
C、（-∞，-1）∪（2，+∞）
D、（2，+∞）
下列函数中，最小正周期为π的偶函数是（　　）
A、y=sin2x
B、y=cos
x
2
C、y=sin2x+cos2x
D、y=
1-tan2x
1+tan2x
已知变量x、y满足条件
x≥1
x-y≤0
x+2y-9≤0
，则2x+y的最大值是（　　）
A、3B、6C、9D、12
已知直线l的参数方程为
x=-10+t
y=t
 （t为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，圆C的极坐标方程为ρ2-4ρsinθ+2=0．
（Ⅰ）把圆C的极坐标方程化为直角坐标方程；
（Ⅱ）将直线l向右平移h个单位，所得直线l′与圆C相切，求h．
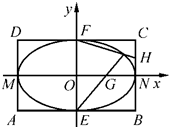如图，矩形ABCD中，|AB|=4，|BC|=2，E，F，M，N分别是矩形四条边的中点，G，H分别是线段ON，CN的中点．
（Ⅰ）证明：直线EG与FH的交点L在椭圆Ω：
x2
4
+y2=1上；
（Ⅱ）设直线l：y=x+m（-1≤m≤1）与椭圆Ω：
x2
4
+y2=1有两个不同的交点P，Q，直线l与矩形ABCD有两个不同的交点S，T，求
|PQ|
|ST|
的最大值及取得最大值时m的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网