题目内容
已知
=(1,1),
=(-2,2),
=(2,k).
(1)若(
-
)∥
,求k的值.
(2)若
⊥
,求k的值.
(3)若
与
的夹角为锐角,求k的取值范围.
| a |
| b |
| c |
(1)若(
| a |
| b |
| c |
(2)若
| a |
| c |
(3)若
| a |
| c |
考点:平面向量数量积的运算,平面向量共线(平行)的坐标表示
专题:平面向量及应用
分析:(1)求出
-
,然后利用向量平行的坐标运算
求k的值.
(2)通过
⊥
,数量积为0,即可求k的值.
(3)若
与
的夹角为锐角,数量积为正值,即可求k的取值范围.
| a |
| b |
| c |
(2)通过
| a |
| c |
(3)若
| a |
| c |
解答:
解:(1)
=(1,1),
=(-2,2),
=(2,k).
∴
-
=(3,-1),(
-
)∥
,
∴-2=3k,∴k=-
.
(2)
=(1,1),
=(2,k),
⊥
,2+k=0,∴k=-2.
(3)
与
的夹角为锐角,∴
•
>0,即2+k>0,∴k>-2.
| a |
| b |
| c |
∴
| a |
| b |
| a |
| b |
| c |
∴-2=3k,∴k=-
| 2 |
| 3 |
(2)
| a |
| c |
| a |
| c |
(3)
| a |
| c |
| a |
| c |
点评:本题考查向量的基本运算,向量的夹角以及数量积的运算,考查计算能力.

练习册系列答案
相关题目
下列函数中,最小正周期为π的偶函数是( )
| A、y=sin2x | ||
B、y=cos
| ||
| C、y=sin2x+cos2x | ||
D、y=
|
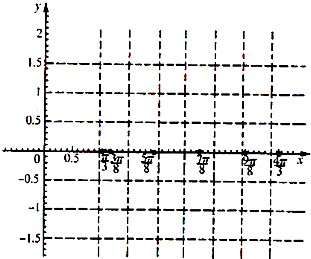 已知函数f(x)=
已知函数f(x)=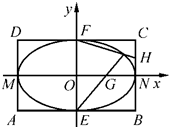 如图,矩形ABCD中,|AB|=4,|BC|=2,E,F,M,N分别是矩形四条边的中点,G,H分别是线段ON,CN的中点.
如图,矩形ABCD中,|AB|=4,|BC|=2,E,F,M,N分别是矩形四条边的中点,G,H分别是线段ON,CN的中点.