题目内容
（1）设向量
、
不共线，已知
=2
+k
，
=
+
，
=
-2
，且A、B、D三点共线，求实数k的值．
（2）已知
=2
-3
，
=2
+3
，其中
，
不共线，向量
=2
-9
，问是否存在这样的实数λ，μ，使
=λ
+μ
与
共线．
| a |
| b |
| AB |
| a |
| b |
| BC |
| a |
| b |
| CD |
| a |
| b |
（2）已知
| a |
| e1 |
| e2 |
| b |
| e1 |
| e2 |
| e1 |
| e2 |
| c |
| e1 |
| e2 |
| d |
| a |
| b |
| c |
考点：平行向量与共线向量,平面向量数量积的运算
专题：平面向量及应用
分析：（1）由题意可得向量
和
共线，存在实数λ，使
=λ
，得关于m，λ的方程组，解之可得．
（2）假设则存在实数k，使
=k
，得到2（λ+μ）
-3（λ-μ）
=k（2
-9
），求出λ=-k，μ=2k，则说明假设成立．
| AB |
| BD |
| AB |
| BD |
（2）假设则存在实数k，使
| d |
| c |
| e1 |
| e2 |
| e1 |
| e2 |
解答：
解：（1）∵
=2
+k
，
=
+
，
=
-2
，
∴
=
+
=
+
+
-2
=2
-
，
由题意可得向量
和
共线，存在实数λ，使
=λ
即2
+k
=λ（2
-
），
故可得2=2λ，k=-λ
解得k=-1．
（2）∵
=2
-3
，
=2
+3
，其中
，
不共线，
∴
=λ
+μ
=λ（2
-3
）+μ（2
+3
）=2（λ+μ）
-3（λ-μ）
，
∵
=2
-9
，
若
，
共线，假设则存在实数k，使
=k
∴2（λ+μ）
-3（λ-μ）
=k（2
-9
），
故可得，λ+μ=k，μ-λ=3k
解得λ=-k，μ=2k，
所以存在这样的实数λ，μ，使
=λ
+μ
与
共线．
| AB |
| a |
| b |
| BC |
| a |
| b |
| CD |
| a |
| b |
∴
| BD |
| BC |
| CD |
| a |
| b |
| a |
| b |
| a |
| b |
由题意可得向量
| AB |
| BD |
| AB |
| BD |
即2
| a |
| b |
| a |
| b |
故可得2=2λ，k=-λ
解得k=-1．
（2）∵
| a |
| e1 |
| e2 |
| b |
| e1 |
| e2 |
| e1 |
| e2 |
∴
| d |
| a |
| b |
| e1 |
| e2 |
| e1 |
| e2 |
| e1 |
| e2 |
∵
| c |
| e1 |
| e2 |
若
| c |
| d |
| d |
| c |
∴2（λ+μ）
| e1 |
| e2 |
| e1 |
| e2 |
故可得，λ+μ=k，μ-λ=3k
解得λ=-k，μ=2k，
所以存在这样的实数λ，μ，使
| d |
| a |
| b |
| c |
点评：本题主要考查了向量共线的问题，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
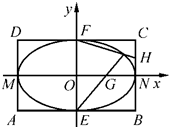如图，矩形ABCD中，|AB|=4，|BC|=2，E，F，M，N分别是矩形四条边的中点，G，H分别是线段ON，CN的中点．
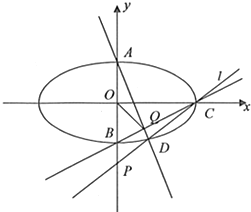如图，已知连接椭圆