题目内容
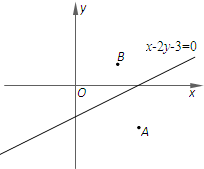 已知⊙P经过A(3,-2)、B(2,1)两点,圆心P在直线x-2y-3=0上.
已知⊙P经过A(3,-2)、B(2,1)两点,圆心P在直线x-2y-3=0上.(1)求⊙P的方程;
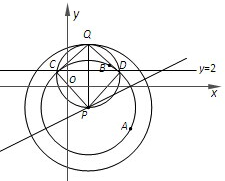
(2)设点Q(a,b)是⊙P外一点,以PQ为直径的圆与⊙P相交于C、D两点,若QC=QD=2,且C、D所在的直线方程为y=
| 2 |
| 3 |
考点:直线和圆的方程的应用
专题:综合题
分析:(1)根据圆的性质,算出AB的垂直平分线方程,与直线x-2y-3=0联解得出圆心P,求出圆的C的半径,从而可得⊙P的方程;
(2)由圆的知识可知:以PQ为直径的圆与⊙P的两个交点C,D,即为过Q点作⊙P的两条切线的切点,可得Q点在以P为圆心,3为半径的圆上运动,确定QP∥y轴,即可得出结论.
(2)由圆的知识可知:以PQ为直径的圆与⊙P的两个交点C,D,即为过Q点作⊙P的两条切线的切点,可得Q点在以P为圆心,3为半径的圆上运动,确定QP∥y轴,即可得出结论.
解答:
 解:(1)∵⊙P经过点A(3,-2)、B(2,1)两点,
解:(1)∵⊙P经过点A(3,-2)、B(2,1)两点,
∴点P在线段AB的垂直平分线y=
x-
又∵圆心P在直线x-2y-3=0上
∴联解得P(1,-1)
圆C的半径r=|AP|=
=
,
∴⊙P的方程是(x-)2+(y+1)2=5;
(2)由圆的知识可知:以PQ为直径的圆与⊙P的两个交点C,D,即为过Q点作⊙P的两条切线的切点.
由QC=2,CP=
,可知QP=3,
∴Q点在以P为圆心,3为半径的圆上运动,
∵QP⊥CD,CD∥x轴,
∴QP∥y轴,
∴a=1,b=2.
 解:(1)∵⊙P经过点A(3,-2)、B(2,1)两点,
解:(1)∵⊙P经过点A(3,-2)、B(2,1)两点,∴点P在线段AB的垂直平分线y=
| 1 |
| 3 |
| 4 |
| 3 |
又∵圆心P在直线x-2y-3=0上
∴联解得P(1,-1)
圆C的半径r=|AP|=
| (3-1)2+(-2+1)2 |
| 5 |
∴⊙P的方程是(x-)2+(y+1)2=5;
(2)由圆的知识可知:以PQ为直径的圆与⊙P的两个交点C,D,即为过Q点作⊙P的两条切线的切点.
由QC=2,CP=
| 5 |
∴Q点在以P为圆心,3为半径的圆上运动,
∵QP⊥CD,CD∥x轴,
∴QP∥y轴,
∴a=1,b=2.
点评:本题给出经过A、B两点的圆的圆心在已知直线上,求圆的方程,着重考查了圆的方程、直线与圆的位置关系等知识,属于中档题.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
已知-1和2是函数y=x2+bx+c的两个零点,则不等式bx2+bx-c<0的解集为( )
| A、(-1,2) |
| B、(-2,1) |
| C、(-∞,-1)∪(2,+∞) |
| D、(2,+∞) |
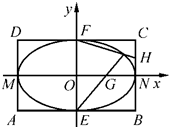 如图,矩形ABCD中,|AB|=4,|BC|=2,E,F,M,N分别是矩形四条边的中点,G,H分别是线段ON,CN的中点.
如图,矩形ABCD中,|AB|=4,|BC|=2,E,F,M,N分别是矩形四条边的中点,G,H分别是线段ON,CN的中点.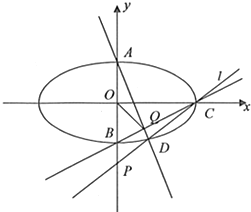 如图,已知连接椭圆
如图,已知连接椭圆