题目内容
已知
=（2cosx，1），
=（cosx，
sin2x+m），f（x）=
•
；
（1）求函数在[0，π]上的单调增区间；
（2）当x∈[0，
]时，f（x）的最大值为4，求实数m的值．（提示：
•
=x1x2+y1y2）
| a |
| b |
| 3 |
| a |
| b |
（1）求函数在[0，π]上的单调增区间；
（2）当x∈[0，
| π |
| 6 |
| a |
| b |
考点：三角函数中的恒等变换应用,平面向量数量积的运算
专题：常规题型,三角函数的图像与性质
分析：根据向量的内积运算，利用两角和的正弦公式化成正弦函数的标准形式，然后根据正弦函数的单调性与最值求函数f（x）的单调区间与最值．
解答：
解：依题意得：
f（x）=
•
=2cos2x+
sin2x+m
=1+cos2x+
sin2x+m
=2sin（2x+
）+1+m
（1）令-
+2kπ≤2x+
≤2kπ+
，得
kπ-
≤x≤kπ+
（k∈Z）
∴f（x）在[0，π]上的单调增区间为[0，
]，[
，π]．
（2）∵x∈[0，
]，∴
≤2x+
≤
∴
≤sin(2x+
)≤1
∴当2x+
=
时，f（x）max=2+m+1
依题意得：3+m=4，∴m=1．
f（x）=
| a |
| b |
| 3 |
=1+cos2x+
| 3 |
=2sin（2x+
| π |
| 6 |
（1）令-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
kπ-
| π |
| 3 |
| π |
| 6 |
∴f（x）在[0，π]上的单调增区间为[0，
| π |
| 6 |
| 2π |
| 3 |
（2）∵x∈[0，
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
∴
| 1 |
| 2 |
| π |
| 6 |
∴当2x+
| π |
| 6 |
| π |
| 2 |
依题意得：3+m=4，∴m=1．
点评：本题考查了向量的内积运算、两角和的正弦公式及三角函数的性质，解题的关键是把函数f（x）化成正弦函数的标准形式．
练习册系列答案
相关题目
若函数f（x）=loga（2x2+x）（a＞0，a≠1）在区间（
，1）内恒有f（x）＞0，则f（x）的单调递增区间是（ ）
| 1 |
| 2 |
A、（-∞，-
| ||
B、（-
| ||
C、（-∞，-
| ||
| D、（0，+∞） |
已知函数f（x）=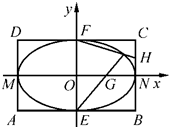
如图，矩形ABCD中，|AB|=4，|BC|=2，E，F，M，N分别是矩形四条边的中点，G，H分别是线段ON，CN的中点．