题目内容
19．函数f（x）=log3x+x-3的零点所在的区间是（ ）| A． | （0，1） | B． | （1，2） | C． | （2，3） | D． | （3，+∞） |
分析 求出函数的定义域，判断连续性，求得 f（2）•f（3）＜0，根据函数的零点的判定定理，可得函数零点所在的大致区间．
解答 解：∵函数f（x）=log3x+x-3，定义域为：x＞0；函数是连续函数，
∴f（2）=log32+2-3＜0，f（3）=log33+3-3=1＞0，
∴f（2）•f（3）＜0，根据函数的零点的判定定理，
故选：C．
点评 本题主要考查函数的零点的判定定理的应用，求函数的值，属于基础题．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
9．近日，我辽宁舰航母与3艘编号不同的导弹驱逐舰艇、2艘编号不同的护卫舰艇开展跨海区训练和编队试验任务，若在某次编队试验中，要求辽宁舰航母前、后、左、右位置均有舰艇，且同一类舰艇不在相同位置（两艘舰艇在同一位置视为一种编队方式），则编队方式有（ ）
| A． | 36种 | B． | 72种 | C． | 144种 | D． | 288种 |
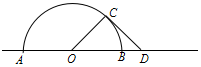某公园内直线道路旁有一半径为10米的半圆形荒地（圆心O在道路上，AB为直径），现要在荒地的基础上改造出一处景观．在半圆上取一点C，道路上B点的右边取一点D，使OC垂直于CD，且OD的长不超过20米．在扇形区域AOC内种植花卉，三角形区域OCD内铺设草皮．已知种植花卉的费用每平方米为200元，铺设草皮的费用每平方米为100元．
7．直线$\frac{x}{a}-\frac{y}{b}=1$在y轴上的截距是（ ）
| A． | a | B． | b | C． | -a | D． | -b |
4．记a=sin1，b=sin2，c=sin3，则（ ）
| A． | c＜b＜a | B． | c＜a＜b | C． | a＜c＜b | D． | a＜b＜c |
11．已知函数f（x）=ax-1（a＞0且a≠1）的图象过定点A，则点A为（ ）
| A． | （0，-1） | B． | （0，1） | C． | （-1，1） | D． | （1，1） |
如图正方体ABCD-A1B1C1D1，M，N分别为A1D1和AA1的中点，则下列说法中正确的个数为（ ）