题目内容
8.已知函数f(x)=$\left\{\begin{array}{l}{2sin\frac{π}{6}x,x≤2000}\\{x-1000,x>2000}\end{array}\right.$,则f(f(2016))=( )| A. | $\sqrt{3}$ | B. | -$\sqrt{3}$ | C. | 1 | D. | -1 |
分析 利用分段函数的意义即可得出.
解答 解:∵函数f(x)=$\left\{\begin{array}{l}{2sin\frac{π}{6}x,x≤2000}\\{x-1000,x>2000}\end{array}\right.$,
∴f(2016)=2016-1000=1016,
∴f(f(2016))=f(1016)=2sin$\frac{1016π}{6}$=2$sin(168π+\frac{4π}{3})$=-2$sin\frac{π}{3}$=-$\sqrt{3}$.
故选:B.
点评 本题考查了分段函数的意义及其求值,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
13.若实数x、y满足约束条件$\left\{\begin{array}{l}{2x-y-2≤0}\\{2x+y-4≥0}\\{y≤2}\end{array}\right.$,则$\frac{x}{y}$的取值范围是( )
| A. | [$\frac{2}{3}$,2] | B. | [$\frac{1}{2}$,$\frac{3}{2}$] | C. | [$\frac{3}{2}$,2] | D. | [1,2] |
7.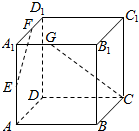 如图,在正方体ABCD-A1B1C1D1中,E、F、G分别是AA1,A1D1,A1B1的中点,则异面直线EF与CG所成的角等于( )
如图,在正方体ABCD-A1B1C1D1中,E、F、G分别是AA1,A1D1,A1B1的中点,则异面直线EF与CG所成的角等于( )
 如图,在正方体ABCD-A1B1C1D1中,E、F、G分别是AA1,A1D1,A1B1的中点,则异面直线EF与CG所成的角等于( )
如图,在正方体ABCD-A1B1C1D1中,E、F、G分别是AA1,A1D1,A1B1的中点,则异面直线EF与CG所成的角等于( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |