题目内容
3.设全集U=R,集合A={x|lgx>0},B={x|2x<4}.( 1)求A∪B;
(2)若集合C={x|2x-a>0},满足A⊆C,求实数a的取值范围.
分析 (1)利用指数函数与对数的单调性化简集合A,B,再利用集合的运算性质即可得出;
(2)由2x-a>0,可得C=$(\frac{a}{2},+∞)$.利用A⊆C,可得$\frac{a}{2}$≤1,解出即可得出.
解答 解:(1)由lgx>0,解得x>1,∴集合A={x|lgx>0}=(1,+∞),
由2x<4,解得x<2.
∴B={x|2x<4}=(-∞,2).
∴A∪B=R.
(2)由2x-a>0,解得x$>\frac{a}{2}$,∴C=$(\frac{a}{2},+∞)$.
∵A⊆C,
∴$\frac{a}{2}$≤1,
解得a≤2.
∴实数a的取值范围是(-∞,2].
点评 本题考查了指数函数与对数的单调性、集合的运算性质、不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
14.已知体积为V的三棱柱ABC-A1B1C1,P为棱BB1上除B,B1两点外的任意一点,则四棱锥P-AA1C1C的体积等于( )
| A. | $\frac{V}{2}$ | B. | $\frac{V}{3}$ | C. | $\frac{2V}{3}$ | D. | $\frac{V}{4}$ |
11.已知函数f(x)=(a+2)x-2是幂函数,则f(a)的值为( )
| A. | 1 | B. | -1 | C. | ±1 | D. | 0 |
8.已知函数f(x)=$\left\{\begin{array}{l}{2sin\frac{π}{6}x,x≤2000}\\{x-1000,x>2000}\end{array}\right.$,则f(f(2016))=( )
| A. | $\sqrt{3}$ | B. | -$\sqrt{3}$ | C. | 1 | D. | -1 |
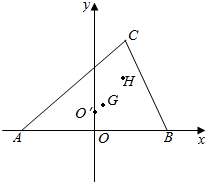 如图,A,B,C的坐标分别为(-$\frac{c}{2}$,0),($\frac{c}{2}$,0),(m,n),G,O′,H分别为△ABC的重心,外心,垂心.
如图,A,B,C的坐标分别为(-$\frac{c}{2}$,0),($\frac{c}{2}$,0),(m,n),G,O′,H分别为△ABC的重心,外心,垂心.