题目内容

已知点O是边长为1的等边三角形ABC的中心，则（
OA
+
OB
）•（
OA
+
OC
）=
 
．
考点：平面向量数量积的运算
专题：平面向量及应用
分析：取边长为1的等边三角形ABC的边AB的中点为D，边AC的中点为E，则由题意可得
OA
+
OB
=2
OD
，
OA
+
OC
=2
OE
．求得∠AOD=∠AOE=
π
3
，再根据OD=OE=
3
6
，利用两个向量的数量积的定义求得（
OA
+
OB
）•（
OA
+
OC
）的值．
解答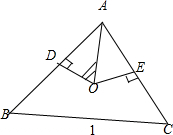： 解：取边长为1的等边三角形ABC的边AB的中点为D，边AC的中点为E，则由题意可得
OA
+
OB
=2
OD
，
OA
+
OC
=2
OE
．
而由等边三角形的性质可得，OA=2OD，OD⊥AB，∴∠AOD=
π
3
，同理可得，∠AOE=
π
3
．
再根据OD=OE=
1
3
•
3
2
=
3
6
，可得（
OA
+
OB
）•（
OA
+
OC
）=2•
OD
•2
OE
=4
OD
•
OE
=4×
3
6
×
3
6
×cos
2π
3
=-
1
6
，
故答案为：-
1
6
．
点评：本题主要考查两个向量的加减法的法则，以及其几何意义，两个向量的数量积的定义，属于基础题．
练习册系列答案
相关题目
根据图中5个图形及相应点的个数的变化规律，归纳猜测第n个图形中的点数an=
 
．
给定下列四个命题：
①“x=
π
3
”是“sinx=
3
2
”的充分不必要条件；
②若“p∨q”为真，则“p∧q”为真；
③若a＜b，则am2＜bm2．
④若集合A∪B=A，则A?B．
其中为真命题的是
 
（填上所有正确命题的序号）
如图是函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，-π＜φ＜π），x∈R的部分图象，则函数f（x）的最小正周期为
 
；函数f（x）的解析式为
 
．
平面区域
x-y≥0
x+y≤4
y≥-2
内的点使（x-2）2+（y+2）2≤1的概率是
 
．
函数y=-（x2+x-c）•ex在区间[-3，2]上不单调，则实数c的取值范围是
 
．
已知点（x，y）满足x2-2x+y2=0，则4x+3y的最大值为
 
，最小值为
 
．
已知三棱锥的三视图如图所示，其中侧视图为直角三角形，俯视图为等腰直角三角形，则此三棱锥的体积等于（　　）
A、
2
2
3
B、
4
3
3
C、
8
3
3
D、8
3
若（x+
1
2x
）n的展开式中的二项式系数之和为256，则展开式中x4的系数为（　　）
A、6B、7C、8D、9

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网