题目内容
 一个盒子中装有大量形状大小一样但重量不尽相同的小球,从中随机抽取50个作为样本,称出它们的重量(单位:克),重量分组区间为(5,15],(15,25],(25,35],(35,45],由此得到样本的重量频率分布直方图,如图.
一个盒子中装有大量形状大小一样但重量不尽相同的小球,从中随机抽取50个作为样本,称出它们的重量(单位:克),重量分组区间为(5,15],(15,25],(25,35],(35,45],由此得到样本的重量频率分布直方图,如图.(1)求a的值;
(2)根据样本数据,试估计盒子中小球重量的平均值;
(注:设样本数据第i组的频率为pi,第i组区间的中点值为xi(i=1,2,3,…,n),则样本数据的平均值为
. |
| X |
(3)从盒子中随机抽取3个小球,其中重量在(5,15]内的小球个数为ξ,求ξ的分布列和数学期望.
考点:离散型随机变量的期望与方差,频率分布直方图
专题:概率与统计
分析:(1)由频率分布直方图所给的数据能求出a.
(2)先由频率直方图的数据求出50个样本小球重量的平均值,由样本估计总体,可估计盒子中小球重量的平均值.
(3)利用样本估计总体,该盒子中小球重量在(5,15]内的概率为0.2,且ξ~B(3,
).ξ的取值为0,1,2,3,由此能求出ξ的分布列和数学期望.
(2)先由频率直方图的数据求出50个样本小球重量的平均值,由样本估计总体,可估计盒子中小球重量的平均值.
(3)利用样本估计总体,该盒子中小球重量在(5,15]内的概率为0.2,且ξ~B(3,
| 1 |
| 5 |
解答:
解:(1)由题意,得(0.02+0.032+a+0.018)×10=1,…(1分)
解得a=0.03.…(2分)
(2)50个样本小球重量的平均值为
=0.2×10+0.32×20+0.3×30+0.18×40=24.6(克).…(3分)
由样本估计总体,可估计盒子中小球重量的平均值约为24.6克.…(4分)
(3)利用样本估计总体,该盒子中小球重量在(5,15]内的概率为0.2,
则ξ~B(3,
).…(5分)
ξ的取值为0,1,2,3,…(6分)
P(ξ=0)=
(
)3=
,
P(ξ=1)=
(
)(
)2=
,
P(ξ=2)=
(
)2(
)=
,
P(ξ=3)=
(
)3=
.…(10分)
∴ξ的分布列为:
…(11分)
∴Eξ=0×
+1×
+2×
+3×
=
.…(12分)
解得a=0.03.…(2分)
(2)50个样本小球重量的平均值为
. |
| x |
由样本估计总体,可估计盒子中小球重量的平均值约为24.6克.…(4分)
(3)利用样本估计总体,该盒子中小球重量在(5,15]内的概率为0.2,
则ξ~B(3,
| 1 |
| 5 |
ξ的取值为0,1,2,3,…(6分)
P(ξ=0)=
| C | 0 3 |
| 4 |
| 5 |
| 64 |
| 125 |
P(ξ=1)=
| C | 1 3 |
| 1 |
| 5 |
| 4 |
| 5 |
| 48 |
| 125 |
P(ξ=2)=
| C | 2 3 |
| 1 |
| 5 |
| 4 |
| 5 |
| 12 |
| 125 |
P(ξ=3)=
| C | 3 3 |
| 1 |
| 5 |
| 1 |
| 125 |
∴ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
∴Eξ=0×
| 64 |
| 125 |
| 48 |
| 125 |
| 12 |
| 125 |
| 1 |
| 125 |
| 3 |
| 5 |
点评:本题考查频率分布直方图的应用,考查离散型随机变量的分布列和数学期望的求法,是中档题,在历年高考中都是必考题型之一.

练习册系列答案
相关题目
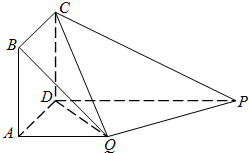 在如图所示的多面体中,四边形ABCD为正方形,四边形ADPQ是直角梯形,AD⊥DP,CD⊥平面ADPQ,AB=AQ=
在如图所示的多面体中,四边形ABCD为正方形,四边形ADPQ是直角梯形,AD⊥DP,CD⊥平面ADPQ,AB=AQ=