题目内容
在△ABC中,已知sinB,sinA,sinC成等差数列,且b,a,c成等比数列,则△ABC的形状是 .
考点:余弦定理,正弦定理
专题:解三角形
分析:根据题意利用等差数列与等比数列的性质列出关系式,再利用正弦定理化简得到sinA=sinB=sinC,利用正弦定理得到a=b=c,即可确定出三角形为等边三角形.
解答:
解:∵在△ABC中,sinB,sinA,sinC成等差数列,且b,a,c成等比数列,
∴2sinA=sinB+sinC,a2=bc,
利用正弦定理化简得:sin2A=sinBsinC,
把sinA=
(sinB+sinC)代入得:
(sinB+sinC)2=sinBsinC,
整理得:(sinB-sinC)2=0,即sinB-sinC=0,
∴sinB=sinC,即sinA=sinB=sinC,
∴a=b=c,
则△ABC为等边三角形,
故答案为:等边三角形
∴2sinA=sinB+sinC,a2=bc,
利用正弦定理化简得:sin2A=sinBsinC,
把sinA=
| 1 |
| 2 |
| 1 |
| 4 |
整理得:(sinB-sinC)2=0,即sinB-sinC=0,
∴sinB=sinC,即sinA=sinB=sinC,
∴a=b=c,
则△ABC为等边三角形,
故答案为:等边三角形
点评:此题考查了正弦、余弦定理,等差、等比数列的性质,以及完全平方公式的运用,熟练掌握定理是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
函数y=
的定义域为( )
| 1-lnx |
| A、(0,e] |
| B、(-∞,e] |
| C、(0,10] |
| D、(-∞,10] |
下列说法正确的是( )
| A、“f(0)=0”是“函数f(x)是奇函数”的充要条件 | ||||||||||||||||||
B、“向量
| ||||||||||||||||||
| C、“?x∈R,x2+1>0”的否定是“?x0∈R,x02+1<0” | ||||||||||||||||||
D、“若a=
|
函数y=
的定义域为( )
| ||
| lg(2x-2) |
| A、[1,2] | ||||
| B、(1,2] | ||||
C、(1,
| ||||
D、[1,
|
下列函数是奇函数的是( )
A、y=x -
| ||
| B、y=2x2-3 | ||
C、y=x
| ||
| D、y=x2,x∈[0,1] |
 如图,直线x=±π,y=±1围成的矩形区域内有一段余弦曲线y=-cosx,任意地向矩形投掷飞镖,则飞镖落入阴影区域的概率是
如图,直线x=±π,y=±1围成的矩形区域内有一段余弦曲线y=-cosx,任意地向矩形投掷飞镖,则飞镖落入阴影区域的概率是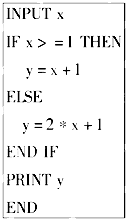 读程序,完成下列题目:程序如图:
读程序,完成下列题目:程序如图: