题目内容
函数y=
的定义域为（ ）
| ||
| lg(2x-2) |
| A、[1，2] | ||||
| B、（1，2] | ||||
C、(1，
| ||||
D、[1，
|
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：根据函数成立的条件即可求函数的定义域．
解答：
解：要使函数有意义则
，
即
，则
，
解得1＜x≤2且x≠
，
故函数的定义域为(1，
)∪(
，2]，
故选：C
|
即
|
|
解得1＜x≤2且x≠
| 3 |
| 2 |
故函数的定义域为(1，
| 3 |
| 2 |
| 3 |
| 2 |
故选：C
点评：本题主要考查函数的定义域的求解，要求熟练掌握常见函数成立的条件
练习册系列答案
一线名师权威作业本系列答案
相关题目
已知向量
=（1，-1），
=（2，m），若
⊥
，则m=（ ）
| a |
| b |
| a |
| b |
| A、-2 | ||
B、-
| ||
C、
| ||
| D、2 |
非空数集A={a1，a2，a3，…，an}（n∈N*，an）中，所有元素的算术平均数记为E（A），即E（A）=
．若非空数集B满足下列两个条件：
①B⊆A；
②E（B）=E（A），则称B为A的一个“保均值子集”．
据此，集合{1，2，3，4，5}的“保均值子集”的概率是（ ）
| a1+a2+a3+…+an |
| n |
①B⊆A；
②E（B）=E（A），则称B为A的一个“保均值子集”．
据此，集合{1，2，3，4，5}的“保均值子集”的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
已知集合A={x|x2-3x-4≤0}，B={x|x=
，x∈Z，k∈Z}，则A∩B=（ ）
| 3 |
| 2k-1 |
| A、{-1，1} |
| B、{-1，1，3} |
| C、{-3，-1，1} |
| D、{-3，-1，1，3} |
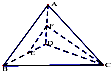如图，在三棱锥A-BCD中，BC=CD=DB，AB=AC=AD；E，F为棱BD，AD的中点，若EF⊥CF，则直线BD与平面ACD所成的角为