题目内容
令f(x)=
,则:f(1)+f(2)+…+f(2011)+f(
)+f(
)+…+f(
)+f(1)= .
| 1 |
| x+1 |
| 1 |
| 2011 |
| 1 |
| 2010 |
| 1 |
| 2 |
考点:函数的值
专题:函数的性质及应用
分析:由已知得f(x)+f(
)=
+
=1,由此能求出f(1)+f(2)+…+f(2011)+f(
)+f(
)+…+f(
)+f(1)的值.
| 1 |
| x |
| 1 |
| x+1 |
| 1 | ||
|
| 1 |
| 2011 |
| 1 |
| 2010 |
| 1 |
| 2 |
解答:
解:∵f(x)=
,
∴f(x)+f(
)=
+
=1,
∴f(1)+f(2)+…+f(2011)+f(
)+f(
)+…+f(
)+f(1)
=2011×1
=2011.
故答案:2011.
| 1 |
| x+1 |
∴f(x)+f(
| 1 |
| x |
| 1 |
| x+1 |
| 1 | ||
|
∴f(1)+f(2)+…+f(2011)+f(
| 1 |
| 2011 |
| 1 |
| 2010 |
| 1 |
| 2 |
=2011×1
=2011.
故答案:2011.
点评:本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
把1+(1+x)+(1+x)2+…+(1+x)n展开成关于x的多项式,其各项系数和为an,则an=( )
| A、2n+1-1 |
| B、2n-1 |
| C、2n+2-1 |
| D、与x有关 |
非空数集A={a1,a2,a3,…,an}(n∈N*,an)中,所有元素的算术平均数记为E(A),即E(A)=
.若非空数集B满足下列两个条件:
①B⊆A;
②E(B)=E(A),则称B为A的一个“保均值子集”.
据此,集合{1,2,3,4,5}的“保均值子集”的概率是( )
| a1+a2+a3+…+an |
| n |
①B⊆A;
②E(B)=E(A),则称B为A的一个“保均值子集”.
据此,集合{1,2,3,4,5}的“保均值子集”的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知集合A={x|x2-3x-4≤0},B={x|x=
,x∈Z,k∈Z},则A∩B=( )
| 3 |
| 2k-1 |
| A、{-1,1} |
| B、{-1,1,3} |
| C、{-3,-1,1} |
| D、{-3,-1,1,3} |
已知函数y=f(x)的图象在区间[a,b]上是连续不断的,且满足f(a)•f(b)<0(a,b∈R,a<b),则函数f(x)在(a,b)内( )
| A、无零点 |
| B、有且只有一个零点 |
| C、至少有一个零点 |
| D、无法确定有无零点 |
 已知函数f(x)=
已知函数f(x)=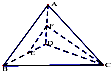 如图,在三棱锥A-BCD中,BC=CD=DB,AB=AC=AD;E,F为棱BD,AD的中点,若EF⊥CF,则直线BD与平面ACD所成的角为
如图,在三棱锥A-BCD中,BC=CD=DB,AB=AC=AD;E,F为棱BD,AD的中点,若EF⊥CF,则直线BD与平面ACD所成的角为